财务可行性评价指标的首要功能就是用于评价某个具体的投资项目是否具有财务可行性。在投资决策的实践中，必须对所有已经具备技术可行性的投资备选方案进行财务可行性评价。

根据投资项目中投资方案的数量，可将投资方案分为单一方案和多个方案；根据方案之间的关系，可以分为独立方案、互斥方案和组合或排队方案。

所谓独立方案是指在决策过程中，一组互相分离、互不排斥的方案或单一的方案。在独立方案中，选择某一方案并不排斥选择另一方案。互斥方案是指互相关联、互相排斥的方案，即一组方案中彼此可以相互代替，采纳方案组中的某一方案，就会自动排斥这组方案中的其他方案。因此，互斥方案具有排他性。

一、单一投资项目的财务可行性分析

（1）如果某一投资项目的评价指标同时满足以下条件，则可以断定该投资项目无论从哪个方面都具备财务可行性，或完全具备可行性，应当接受此投资方案。这些条件是：

NPV≥0；NPVR≥0；PI≥1；IRR≥i；PP≤n/2；PP'≤p/2；ROI≥i_r（事先给定）。

（2）如果某一投资项目的评价指标同时不满足上述条件，即同时满足以下条件时，则可以断定该投资方案无论从哪个方面都不具备财务可行性，或完全不具备可行性，应当彻底放弃该投资方案。这些条件是：NPV<0；NPVR<0，Pl n/2；PP'> p/2；ROI< i_r。

（3）如果在评价过程中发现某项目的主要指标处于可行区间，即：NPV≥0；NPVR≥0；PI≥1；IRR≥i；但次要指标处于不可行区间，即：PP> n/2；PP'> p/2或ROI< i_r，则可以断定该项目基本上具有财务可行性。

（4）如果在评价过程中发现某项目出现NPV<0；NPVR<0，PI<1；即使有PP≤n/2；PP'≤p/2或ROI≥i_r，也可以断定该项目基本上不具备财务可行性。

（5）当静态投资回收期或投资利润率的评价结论与净现值等主要指标的评价结论发生矛盾时，应当以主要指标的结论为准。

（6）利用净现值、净现值率、获利指数和内含报酬率指标对同一个独立项目进行评价时，一般不会得出相互矛盾的结论。

二、多个互斥项目的比较与选优

企业在进行投资项目决策时，常常会碰到多个可供选择的投资项目，企业必须从中选择一个项目，这就是互斥项目的投资决策问题。投资决策中的互斥项目决策是指在决策时涉及多个相互排斥、不能同时并存的投资方案。互斥方案决策过程是在每一个入选方案已具备财务可行性的前提下，利用具体决策方法比较各个方案的优劣，利用评价指标从各个备选方案中最终选出一个最优方案的过程。互斥方案决策的方法主要有净现值法、净现值率法、差额投资内含报酬率法和年均净现值法等。所谓净现值法，是指通过比较所有已具备财务可行性投资方案的净现值指标的大小来选择最优方案的方法。该法适用于原始投资额相同且项目计算期相等的多方案比较决策。在此法下，净现值最大的方案为优。所谓净现值率法，是指通过比较所有已具备可行性投资方案的净现值率指标的大小来选择最优方案的方法。该法适用于项目计算期相等且原始投资额相同的多个互斥方案的比较决策。在此法下，净现值率最大的方案为优。在投资额相同的互斥方案比较决策中，采用净现值率法会与净现值法得到完全相同的结论；但投资额不相同时，他们得出的结论可能会不同。所谓差额投资内含报酬率法，是指在两个原始投资额不同方案的差量净现金流量（△NCF）的基础上，计算出差额内含报酬率（△IRR），并与基准折现率进行比较，进而判断方案孰优孰劣的方法。该法适用于两个原始投资额方案不相同，但项目计算期相同的多方案比较决策。当差额内含报酬率指标大于或等于基准折现率或设定折现率时，原始投资额大的方案较优；反之，则原始投资额小的方案为优。年均净现值（年等额净回收额）法，是指通过比较所有投资方案的年均净现值（年等额净回收额）指标的大小来选择最优方案的决策方法。该法适用于原始投资额不同、特别是项目计算期不同的多方案比较决策。在此法下年均净现值（年等额净回收额）最大的方案为优。另外，净现值、内含报酬率、获利指数等方法在互斥方案或非常规方案的应用中可能会得出不同的结果，应该引起注意。

（一）净现值和内含报酬率的比较

在多数情况下，运用净现值和内含报酬率这两种方法得出的结论是相同的。但在以下两种情况下，有时会产生差异。

1.互斥项目

对于常规的独立项目，净现值法和内含报酬率法的结论是完全一致的，但对于互斥项目，有时就会不一致。不一致的原因主要有两个：投资规模不同和现金流量发生的时间不同。

（1）投资规模不同。当一个项目的投资规模大于另一个项目时，规模较小的项目的内含报酬率可能较大但净现值可能较小。例如，假设项目甲的内含报酬率为30%，净现值为100万元，而项目乙的内含报酬率为25%，净现值为220万元。在这两个互斥项目之间进行选择，实际上就是在更多的财富和更高的内含报酬率之间进行选择，很显然，决策者将选择财富。所以，当互斥项目投资规模不同时，应选净现值大的方案而不必考虑内含报酬率的高低。

（2）现金流量发生的时间不同。有的项目早期现金流入量比较大，而有的项目早期现金流人量比较小。之所以会产生现金流量发生时间的问题，是因为“再投资率假设”。即两种方法假定投资项目使用过程中产生的现金流量进行再投资时，会产生不同的报酬率。净现值法假定产生的现金流入量重新投资会产生相当于企业资本成本的利润率，而内含报酬率法却假定现金流入量重新投资产生的利润率与此项目的特定的内含报酬率相同。

【例7-15】假定有两个投资项目A和B，它们的详细资料如表7-5所示。

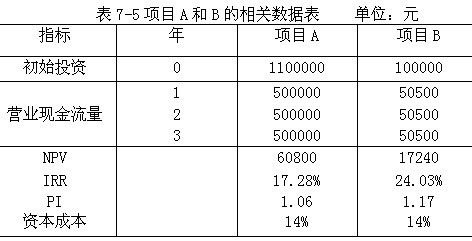
计算在不同贴现率情况下的两个项目的净现值如表7-6所示。

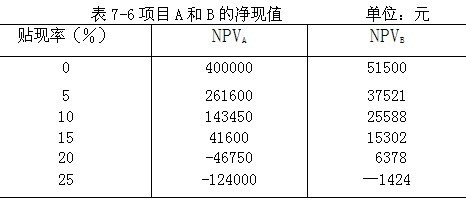
从表7-5可以看出，如果按内含报酬率法应拒绝项目A而采用项目B，如果应用净现值法则应采用项目A而拒绝项目B。产生上述差异的根本原因是内含报酬率法假定项目A前两期产生的现金流量（第1年和第2年的500000元）若进行再投资，则会产生与17.28%相等的报酬率，而项目B前两期的现金流量（第1年和第2年的50500元）若进行再投资则得到24.03%的报酬率。与此相反，净现值法假定前两期产生的现金流量若进行再投资，报酬率应当相等，在本例中是14%，即资本成本。

将表7-6中不同贴现率情况下计算出的净现值绘入图7-1中。

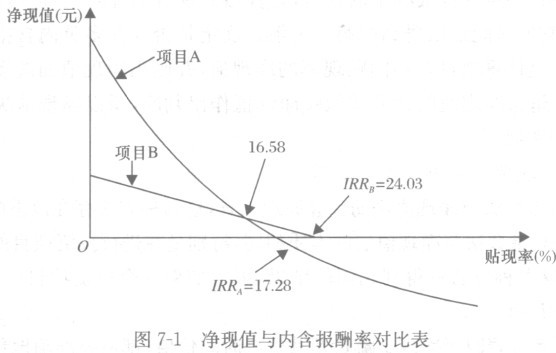
如图7-1所示，两个项目的净现值曲线相交于16.58%处，我们把这一点称为净现值无差异点。如果资本成本小于16.58%，则项目A的净现值要大于项目B，即项目A优于项目B，如果资本成本大于16.58%，则项目B的净现值大于项目A，即项目B优于项目A。因此，在资本成本14%时，且没有资金限量的情况下，项目A虽然投资较多，但净现值也较高，可为企业带来较多的财富，是较优的项目；而当资本成本大于16.58%时，不论用净现值法还是内含报酬率法，都会得出项目B优于项目A的结论。也就是说，净现值总是正确的，而内部报酬率法有时却会得出错误的结论。因此，在无资本限量的情况下，净现值法是一个比较好的方法。

2.非常规项目

非常规项目的现金流量形式在某些方面与常规项目有所不同，如现金流出不发生在期初或者期初和以后各期有多次现金流出等。非常规项目可能会导致净现值决策和内含报酬率决策的结论不一致。

一种比较复杂的情况是：当期望现金流量中一些为正、另一些为负时就会出现多重报酬率的问题。例如，企业付出一笔初始投资后，在项目经营过程中会获得正的现金流量，而在项目结束时需要付出一笔现金进行环境清理；在项目存续期间需要一次或多次大修理的项目也属于这种情况。这种情况下，期望净现金流量可能会出现负的、正的、负的等变化。

一般来说，对于多重报酬率的投资项目，内含报酬率的个数不会多于项目各期期望现金流量中正负号变化的次数。常规项目只有一个内含报酬率，因为各期期望现金流量中正负号只变化了一次，即一笔负的流量后面跟着若干比正流量。

对于存在多重内含报酬率的投资，计算器和现有的计算机程序通常也不能作出识别，它们只能给出碰到的第一个解。确定是否存在多重内含报酬率问题的最好办法是计算项目在不同贴现率的净现值，并画出净现值曲线图。因为这种方法也要进行净现值的计算并依赖净现值作出判断，所以净现值决策规则优于内含报酬率规则。

（二）净现值和获利指数的比较

从获利指数法与净现值法的计算原理来看，这两种方法存在以下的联系：

（1）获利指数法与净现值法的本质相同，特别是在进行投资项目的可行性分析时，采用这两种方法将得到相同的结果，因为如果一个投资项目的NPV＞0，则一定有PI＞1。

（2）两者都着眼于净现金流量及其资金时间价值，都需要准确地预测投资项目有效期内的净现金流量。

（3）在原始投资额不同的两个方案之间进行决策分析时，采用获利指数法与净现值法进行评价，所得结果可能不一致。例如，在表7-5中，A项目和B项目的初始投资额是不同的，在资本成本为14%时，项目A有净现值60800元，获利指数为1.06。项目B有净现值17240元，获利指数为1.17。如果利用净现值法，则应选用项目A，如果利用获利指数，则应选用项目B。

只有在初始投资不同时，净现值和获利指数才会产生差异。由于净现值是用各期现金流量现值减初始投资，是一个绝对数，代表投资的收益或者说是给公司带来的财富，而获利指数是用现金流量现值除以初始投资，是一个相对数，代表投资的效率，因而，评价的结果可能会产生不一致。

最高的净现值符合企业的最大利益，也就是说，净现值越高，企业的收益越大，而获利指数只反映投资回收的程度，而不反映投资回收的多少，在没有资金限量情况下的互斥选择决策中，应选用净现值较大的投资项目。也就是说，当获利指数与净现值得出不同结论时，应以净现值为准。

总之，在无资金限量的情况下，利用净现值法在所有的投资评价中都能作出正确的决策。而利用内含报酬率和获利指数在单一项目决策中也能作出正确的决策，但在互斥选择决策或非常规项目中有时会得出错误的结论。因而，在这三种评价方法中，净现值法仍然是最好的评价方法。

三、固定资产更新决策

固定资产更新是对技术上或经济上不宜继续使用的旧资产，用新的资产更换，或用先进的技术对原有设备进行局部改造。固定资产更新决策主要研究两个问题：一是决定是否更新，即继续使用旧资产还是更换新资产；二是决定选择什么资产来更新。实际上，这两个问题是结合在一起考虑的，如果市场上没有比现有设备更适用的设备，那么就继续使用旧设备。由于旧设备总可以通过修理继续使用，所以更新决策是继续使用旧设备与购置新设备的选择。

（一）更新决策的现金流量分析

更新决策不同于一般的投资决策。一般说来，设备更换并不改变企业的生产能力，不增加企业的现金流入。更新决策的现金流量主要是现金流出。即使有少量的残值变价收人，也属于支出抵减，而非实质上的流入增加。由于只有现金流出，而没有现金流入，就给采用贴现现金流量分析带来了困难。下面给出更新改造投资项目净现金流量的简化公式，可以依此计算固定资产更新改造项目的净现金流量。

1.建设期净现金流量的简化计算公式

如果更新改造投资项目的固定资产投资均在建设期内投入，建设期不为零，且不涉及追加流动资金投资，则建设期的简化计算公式为：

显然，如果建设期为零，公式（2）无效。

2.经营期净现金流量的简化计算公式

如果建设期为零，则经营期净现金流量的简化计算公式为：

公式（3）、（4）中，“因更新改造而增加的折旧”是指按使用新设备发生的年折旧与假定继续使用旧设备应当发生的年折旧的差额，其中旧设备的年折旧不是按其账面原值确定的，而是按更新改造当时旧设备的变价净收入扣除假定可继续使用若干年后的预计净残值，再除以预计可继续使用年限计算出来的。为简化计算，通常假定新设备的使用年限和旧设备的可继续使用年限相等。在这种情况下，因更新改造而增加的折旧的计算公式为：

如果建设期不为零，则公式（3）无效，整个经营期净现金流量均可按公式（4）计算。

（二）固定资产的平均年成本

固定资产的平均年成本是指该资产引起的现金流出的年平均值。如果不考虑资金的时间价值，它是未来使用年限内的现金流出总额与使用年限的比值。如果考虑资金的时间价值，它是未来使用年限内现金流出总现值与年金现值系数的比值，即平均每年的现金流出。

【例7-16】商运公司3年前购入一台小松挖掘机，价值32万元，目前维修成本很高，公司考虑购买一台新的挖掘机代替旧挖掘机，以节约成本。新、旧挖掘机的有关资料如表7-7所示。

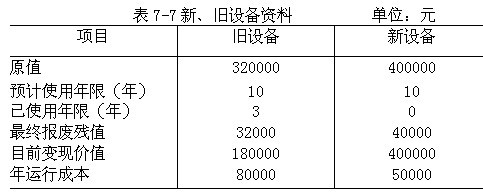
假设两设备的生产能力相同，企业的资本成本为10%，请问该公司是否应该更新设备？

由于没有适当的现金流入，无论哪个方案都不能计算其净现值和内含报酬率，通常在收入相同时，我们认为成本较低的方案是好方案。那么，我们可否通过比较两个方案的总成本来判别方案的优劣呢？仍然不妥，因为旧设备尚可使用7年，而新设备可使用10年，两个方案取得的“产出”并不相同。因此，解决这类问题可直接比较新、旧设备的年平均成本，即获得1年的生产能力所付出的代价，据以判断方案的优劣。

年平均成本的计算有三种方法，现分别介绍如下：

（1）将投资项目现金流出的总现值，按年金现值系数转化为年平均成本。用公式表示为：

（2）在设备各年运行成本相等情况下，可运用年金现值系数、年金终值系数分别将初始投资和残值平均分摊到各年，加各年运行成本，计算年平均成本。用公式表示为：

（3）将残值在初始投资额中减除，视同每年承担相应的利息，然后与净投资额及年运行成本总计，求出年平均成本。用公式表示为：

运用三种方法计算的新设备的年运行成本低于旧设备的年运行成本，所以应该进行更新。

从[例7-16]可以发现：固定资产使用初期运行费用比较低，以后随着设备逐渐陈旧、性能变差，维护、修理、能源消耗逐步增加，运行费便会逐年增加。与此同时，固定资产价值逐渐减少，其占用资金的应计利息会逐年减少。随着时间的递延，运行成本和持有成本呈反方向变化，两者之和呈马鞍形，必然存在一个最经济的使用年限。如图7-2所示。

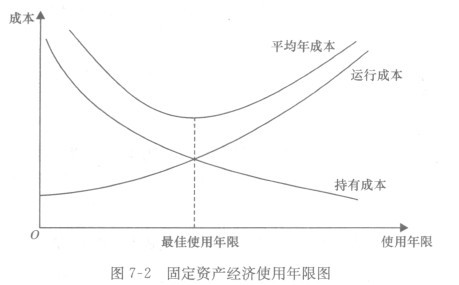
（三）差额净现值法和差额内含报酬率法在更新改造投资决策中的运用

如果新、旧设备未来的使用年限相同，对于固定资产是否更新的决策，一般可以采用差额净现值法或差额内含报酬率法作出判断。

【例7-17】商运公司打算变卖一套尚可使用5年的旧设备，另购置一套新设备来替代它。取得新设备的投资额为180000元，旧设备的折余价值为90000元，其变价净收入为80000元，到第5年年末新设备与继续使用旧设备届时的预计净残值相等。新旧设备的替代将在当年内完成（即更新设备的建设期为零）。使用新设备可使企业每年增加营业收入60000元，增加营业成本30000元。设备采用直线法计提折旧。企业所得税税率为25%，假设与处理旧设备相关的营业税金可以忽略不计，行业基准折现率为9%。

要求：试计算该公司更新设备方案是否可行。

首先，计算该方案的净现金流量。

（1）更新设备继续使用旧设备增加的投资额=180000-80000=100000（元）

（2）每年因更新改造而增加的折旧=100000÷5=20000（元）

（3）每年总成本的变动额=30000+20000=50000（元）

（4）每年营业利润的变动额=60000-50000=10000（元）

（5） 因旧设备提前报废发生的处理固定资产净损失=90000-80000=10000（元）

（6）因更新改造而引起的每年所得税的变动额=10000×25%=2500（元）

（7）第一年因发生处理固定资产净损失而抵减的所得税额=10000×25%=2500（元）

（8）每年因更新改造而增加的净利润=10000-2500=7500（元）

（9）按简化计算公式确定的建设期差量净现金流量为：

（10）按简化计算公式确定的经营期差量净现金流量为：

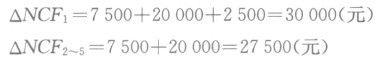
其次，计算差额内含报酬率。

因为各年差额净现金流量不等，所以只能采用逐次测试法。

设折现率为12%，则

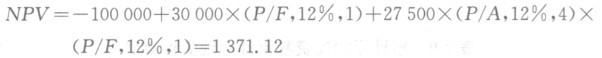
设折现率为15%，则

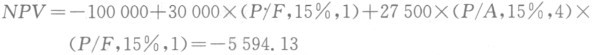
用内插法求出△IRR为12.59%。

因为△IRR＞i（12.5%>9%）所以应当更新设备。

四、资本限量决策

任何企业的资金都有一定限度，不可能投资于所有的可接受项目。当企业可用于投资的资金有限而可供选择的项目很多时，究竟应该选择哪些项目呢?对于这类问题，称之为资本限量决策。在资本限量决策中，待选投资项目很多，决策时一方面应尽可能充分利用可供投资的资本，另一方面又不能超过预定用于投资的资本限额。在这种情况下，可能会有很多的项目搭配方案可供选择。下面把这类方案的决策程序概括如下：

（1）先计算所有方案的NPV及PI。

（2）选择NPV≥0及PI≥1的方案为备选方案。

（3）在资本限量内对各种备选方案进行组合，计算出各种组合的净现值（或获利指数）。

（4）选择净现值最大的投资组合。

【例7-18】设有A、B、C、D、E五个投资项目，有关资料如表7-8所示。若当年可用于投资的资金为600万元，作出投资方案组合决策。

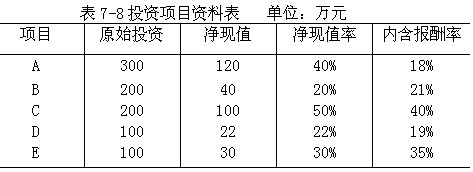
依题意按各方案净现值率的大小排序，并计算累计原始投资和累计净现值数据。如表7-9所示。

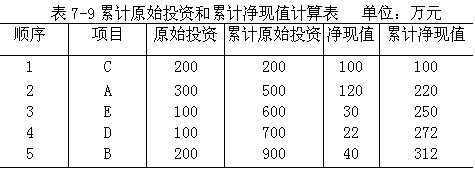
由于限定投资额为600万元，所以C+A+E方案最优。

假定[7-18]的投资额限定为200万元，只能选择C项目，因为C项目可获得100万元净现值，比另一组合E+D的净现值多48万元（100-52）。