任何投资项目都是有风险的，公司在制定资本预算时，不仅要考虑这些风险的大小并将其纳入项目的评估范围，还应在设计项目时尽可能减少这些不确定性。在项目分析中，项目的风险可以分成三个层次：第一层次是项目的特有风险，它可以用项目预期收益率的波动来衡量。通常，项目的特有风险不宜作为项目资本预算时风险的度量。第二个层次是项目的公司风险，可以用项目对于公司未来收益不确定性的影响大小来衡量。因为项目特有风险可以通过与公司其他项目组合而分散，所以要考虑某项目对公司现有项目组合的整体风险产生的影响增量。它不是这个项目的全部风险，而是扣除被项目组合分散掉的剩余部分。第三层次是项目的市场风险，即新项目给股东带来的风险。在项目的公司风险中.股东可以通过多元化组合分散掉一部分风险，剩下的就是完全不可分散的系统风险。因此，唯一影响股东预期收益的是项目的系统风险，而这正是与项目分析相关的风险度量。

一、调整现金流量法

在风险投资决策中，由于各年的现金流量具有不确定性，这就必须进行调整。所谓肯定当量法，就是把不确定的各年现金流量，按照一定的系数（通常称为约当系数）折算为大约相当于肯定的现金流量的数量，然后，利用无风险贴现率作为折现率计算净现值来评价风险投资项目的决策分析方法。其风险调整后净现值的计算公式为：

式中的a_t代表t年现金流量的肯定当量系数，即约当系数。约当系数是肯定的现金流量和与之相当的、不肯定的期望现金流量的比值。用公式表示为：

在进行评价时，可根据各年现金流量风险的大小，选取不同的约当系数。当现金流量为肯定时，可取约当系数为1；当现金流量的风险很小时，可取0.8≤a_t<1；当风险一般时，可取0.4 ≤a_t<0.8；当现金流量风险很大时，可取0≤a_t<0.4。

约当系数的选择，可能会因人而异，敢于冒险的投资者会选用较髙的约当系数，而不愿意冒险的投资者可能选用较低的约当系数。为了防止因投资者的风险偏好不同而造成决策失误，有些企业根据标准离差率来确定约当系数。因为标准离差率是衡量风险大小的一个很好的指标，因而，用它来确定约当系数是合理的。标准离差率与约当系数的经验对照关系如表7-10所示。

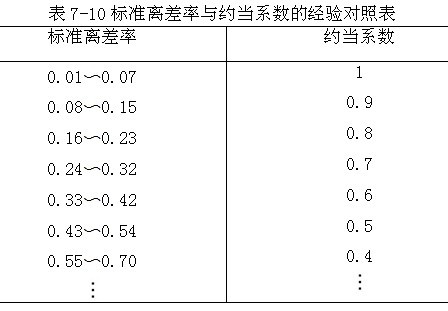
有些时候，也可以对不同的分析人员各自给出的约当系数进行加权平均，用这个加权平均约当系数对未来不确定的现金流量进行折算。在约当系数确定后，决策分析就比较容易了。

【例7-19】假定某公司准备进行一项投资，其各年的预计现金流量和分析人员确定的约定系数如表7-11所示，无风险报酬率为4%，试判断该项目是否可行。

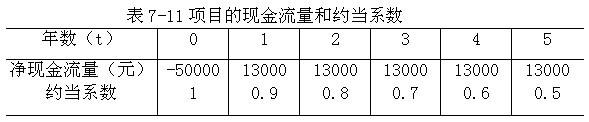
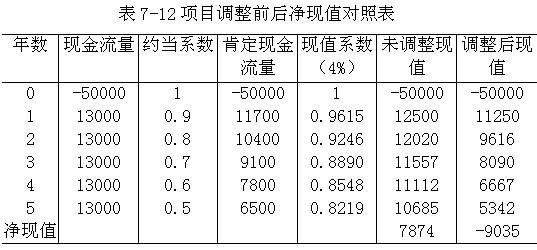
根据表7-11计算调整前现金流量现值及调整后现金流量现值如表7-12所示。

从以上计算可以看出，未调整前净现值为正数（7874元），按风险程度对现金流量进行调整后，计算出的净现值为负数，所以不能进行投资。

调整现金流量法在理论上受到好评。该方法对时间价值和风险价值分别进行调整，先调整风险，然后把肯定现金流量用无风险报酬率进行折现。对不同年份的现金流量，可以根据风险的差别使用不同的约当系数进行调整。

二、风险调整折现率法风险调整折现率的计算公式为：

风险调整折现率法是更为实际、更为常用的风险处置方法。这种方法的基本思路是：对高风险的项目应当采用较高的折现率计算净现值。其风险调整后净现值的计算公式为：

风险调整折现率的计算公式为：

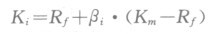
式中的K_i代表项目i按风险调整的贴现率或项目的必要报酬率，R_f代表无风险贴现率，β_i代表项目i的可不分散风险的β系数，K_m代表所有项目平均的贴现率或必要报酬率。

【例7-20】假定某公司目前有两个投资项目可供选择，当前的无风险报酬率为4%，市场平均报酬率为12%，A项目的jS值为1.5，B项目的β值为0.75。各年现金流量资料如表7-13所示。

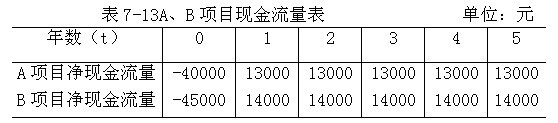
首先，根据上述资料计算A、B项目的风险调整折现率。

A项目的风险调整折现率=4%+1.5×（12%-4%）=16%

B项目的风险调整折现率=4%+0.75×（12%-4%）=10%

其次，根据无风险利率和风险调整折现率计算的调整前后的净现值如表7-14所示。

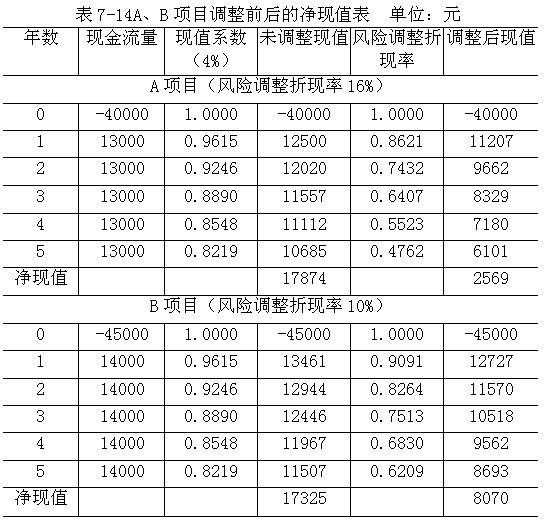
如果不进行折现率调整，两个项目差不多，A项目的净现值（17874元）比B项目的净现值（17325元）高一点，应该说A项目较好；调整后，两个项目有明显的区别，B项目的净现值（8070元）比A项目的净现值（2569元）高很多，显然B项目好。

风险调整折现率法在理论上受到批评，因其用单一的折现率同时完成风险价值调整和时间价值调整。这种做法意味着风险随时间推移而加大，可能与事实不符，夸大远期现金流量的风险。

从实务上看，经常应用的是风险调整折现率法，主要原因是风险调整折现率比约当系数容易估计。此外，大部分财务决策都使用报酬率来决策，调整折现率更符合人们的习惯。

三、概率法

概率法是指通过发生概率来调整各期的现金流量，并计算投资项目的年期望现金流量和期望净现值，进而对风险投资作出评价的一种方法。概率法适用于各期的现金流量相互独立的投资项目。所谓各期的现金流量相互独立，是指前后各期的现金流量互不相关。

运用概率法时，各年的期望现金流量计算公式为：

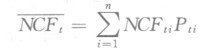
式中的代表第z年的期望净现金流量，代表第t年的第i种结果的净现金流量，P_it代表第t年的第i种结果发生的概率，n代表第t年可能结果的数量。

投资的期望净现值的计算公式为：

式中的代表投资项目的期望净现值，（P/F，i，t）代表贴现率为i、t年的复利现值系数，n代表未来现金流量的期数。