一、物流成本预测的作用

为物流成本决策提供佑据

1.物流成本预测是从客观实际出发，系统地研究物流过程的有关信息资料，并对客观情况作出科学的论断，提出物流过程成本支出的若干可行性方案，为企业决策提供依据。

2.为确定目标成本奠定基础

物流成本预测是物流成本管理的重要组成部分，是制订物流成本预算过程中必不可少的阶段。在物流过程之前必须进行科学的论证，物流成本预测出物流过程中的总支出额，并以此作为计划成本目标考核的依据。

3.减少企业经营的盲目性，降低经营风险

企业为了提高自身的竞争能力，往往转变经营方向，实行多元化的经营战略。如果在决策之前，以物流成本进行分析和预测，就会为决策提供可靠的依据，从而减少因此给企业带来的经营风睑，使企业在激烈的竞争中立于不败之地。

4.是企业制定物流成本目标的依据

企业通过对物流成本的分析和预测，科学地制定出物流成本目标，从而为科学管理物流成本提供依据。

5.是企业扩大经营范围，满足市场需求的重要手段

随着生活水平的不断提高，人们的需求也会不断变化，企业为了适应这种不断变化的需求，就要适时改变经营方式以满足市场需求，这必然会要求企业增加投资。同时，这也要求企业在为了满足市场需求而进行投资之前,要对由于投资而将要增加的成本进行预测，从而采取相应的措施，以适应不断变化的市场需求。

二、物流成本预测的内容与种类

物流成本预测包括库存成本的预测、运输成本的预测、配送成本的预测、包装成本的预测、装卸搬运成本的预测、流通加工成本的预测和物流信息成本的预测等。

按照不同的分类标准，物流成本预测的种类有所不同。通常在进行物流成本预测分类时，可按对象的范围进行分类，按预测的时间长短进行分类，以及按预测目的所用方法不同而进行分类等。

物流成本预测按对象的范围可分为宏观预测和微观预测。宏观预测是指对大系统的综合的、总体的预测，如对整个流通领域物流成本的预测。微观预测是指从单个企业出发，研究预测各个要素的变化预测，如某物流企业对其某项业务成本的预测。宏观预测要求对整个流通领域在物资流通的整个过程中所消耗的成本进行预测；而 微观预测是对个别具体的物流企业物资流通过程中所支付的成本进行预测，如基层企业所做的库存成本、运输成本、配送成本、物流信息成本的预测等。

物流成本预测按时间的长短可分为近期预测和远期预测，亦即短期预测与长期预测。一般将1年或1年以内的预测称为短期预测，短期预测由于预测的时间短，不确定因素和影响因素较少，所以预测结果比较准确；而1年以上的预测统称为长期预测，长期预测由于预测的时间比较长，有许多不确定因素的影响，所以预测结果一般不太精确，需要不断搜集新的信息或数据对预测方案和预测结果进行完善。

物流成本预测按预测目的所用方法不同可分为定性预测和定量预测。定性预测是通过对现象的调査和了解，凭预测者个人的实践经验、理论水平和分析能力，对事物未来的发展所作出的判断。定性预测不要求结果非常准确，只是对事物的发展变化做大致的估计。定性预测法包括经济指标法、调查预测法等。定量预测是根据过 程和现在的资料，运用一定的数学方法，建立预测模型，对现象未来的变化趋势作出预测。定量预测法包括因果回归分析预测法、时间序列分析预测法等。

实际应用中，应从预测对象的发展规律出发，正确地选择和运用预测方法。一般来说，当我们能够收集较多的数据资料时，应当采用定量预测的方法；而当缺乏足够的数据资料时，只能采用定性预测的方法。在实际预测时，往往根据掌握数据的情况采用多种方法同时预测，以获得较为可靠的结论。

三、物流成本预测的方法

（一）直观成本预测法

直观成本预测法又称为判断分析法，是一种定性预测的方法，它是由物流成本预测者通过对市场及其他有关方面的调查而掌握比较全面的资料后，凭借其工作经验和综合能力，预计未来物流成本的一种科学方法。这种方法多数是在缺乏准确数据资料的情况下应用。常用的形式是访问、现场观测、召开座谈会等。这种方法的优点是成本预测费用投资少，成本预测所需的时间短；缺点是成本预测效果的客观性

（二）外推法

外推法是一种定量预测方法，主要是指时间序列预测法（即趋势预测法）。这种方法的基本思路是把时间序列作为随机变量序列的一个样本，应用概率统计的方法，尽可能减少偶然因素的影响，作出在统计意义上的预测。

下面，介绍时间序列预测法中最常用的两种方法——趋势平均法和指数平滑法。

1.趋势平均法

此法建立在过去的成本趋势及其规律性依然不变这一假定之上。其基本计算公式如下：

某期预测值=最后一期平均数+推后期数×最后一期趋势移动平均数

【例3-1】资料：某企业2011年各月的实际物流成本如表3-1所示。

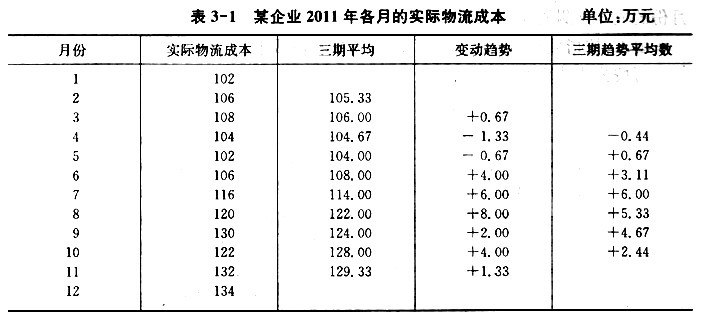
要求：按趋势平均法预测该企业2012年第一季度各月的物流成本（设按三期移动平均）。

根据表3-1的有关数据，可按上述公式进行物流成本的预测：

2012年1月份物流成本=129.33+2 ×2.44= 134.24（万元）

2012年2月份物流成本=129.33+3×2.44=136. 65（万元）

2012 年 3 月份物流成本=129. 33+4×2.44=139. 09（万元）

显然，采用趋势平均法计算若干期的平均数和趋势平均数时，前后各个时期所用的是同一个权数，即认为这些数据对未来的预测值具有同等的影响。因此，用此法预测的 结果与实际情况往往差异较大。为了弥补这一缺陷，可以采用指数平滑法进行预测。

2.指数平滑法

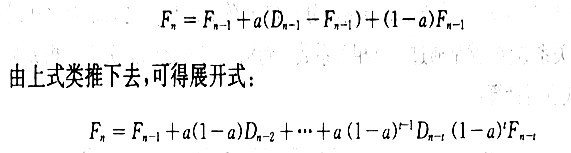
可见,指数平滑法在预测时分别以a、a（l-a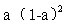）、等系数对过去各期的实际数进行了加权。远期的实际值影响较小，因而其权数也较小；近期的实际值影响较大，因而其权数也较大。显然，这种预测方法更符合客观实际（但a的确定具有较大的主观因素）。

【例3-2】资料：某工厂2011年1〜9月份的实际物流成本分别为：186万元、170万元、180万元、176万元、185万元、180万元、190万元、188万元、188万元：假设1 月份的成本预测值为183万元，a=0.4。

要求：按指数平滑法预测该厂10月份的物流成本。可按公式计算如下：

F1 = 1 830 000（元）

F2 = 0.4×1 860 000+（1-0. 4）×I 830 000 = 1 842 000（元）

F3 = 0.4×1 700 000 +（1 - 0. 4）×1 842 000 = 1 785 200（元）

F4 = 0.4 ×1 800 000 +（1-0. 4）×I 785 200 = 1 791 120（元）

F5 = 0.4 ×1 760 000+（1-0. 4）×1 791 120 = 1 778 672（元）

F6 = 0.4×1 850 000+（1-0.4） × 1 778.672 = 1 807 203. 20（元）

F7 = 0.4× 1 000 000 +（1-0.4）× 1 807 203. 20 = 1 804 321. 92（元）

F8 = 0.4×1 900 000 +（1-0. 4）×1 804 321. 92 = 1 842 593. 15（元）

F9 = 0.4×1 880 000 +（1-0.4）×1 842 593. 15 = 1 857 555. 89（元）

F10 =0.4× 1 910 000+（1-0.4） ×1 857 555. 89 = 1 878 533. 53（元）

从上述计算得出，该厂2011年10月份的物流成本预测值为1 878 533. 53元。

（三）因果分析法

定量分析中的因果法，主要是指回归分析法，它是通过对观察值的统计分析来确定它们之间的联系形式的一种有效的预测方法。

从量的方面来说，事物变化的因果关系可以用一组变量来描述，因为因果关系可以表述为变量之间的依存关系，即自变量与因变量的关系。运用变量之间这种客观 存在着的因果关系，可以使人们对未来状况的预测达到更加准确的程度。

按其影响因素的不同，可分为一元线性回归预测法和多元线性回归预测法。

1.一元线性回归预测法利用线性回归分析法时，要确定自变量x与因变量y之间是否线性相关及其相关程度，判别的方法主要有“散布图法”与“相关系数法”。所谓散布图法，就是将有关 的数据绘制成散布图，然后依据散布图的分布情况判断x与y之间是否存在线性关系；所请相关系数法，就是通过计算相关系数r判别x与y之间的关系。相关系数可按下列公式进行计算：

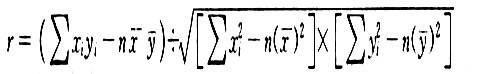
判断标准如表3-2所示。

在确认因变量与自变量之间存在线性关系之后，便可建立回归直线方程：

y = a+ bx

式中y为因变量；x为自变量；a、b为回归系数。根据最小二乘法原理，可得到求a、b的公式：

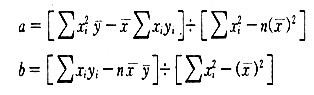
【例3-3】资料：假设某企业物流部门2011年各月份实际发生的运输小时和运输设备维修成本如表3-3所示。

要求：采用回归分析法预测该车间2002年第一季度的机器维修成本。

假设以y代表运输设备维修成本,x代表工作时间，根据上表提供的资料计算如表3-4所示。

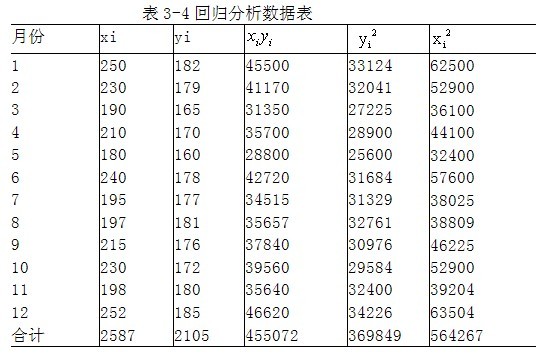
为判断X与y之间是否存在着线性联系，应先计算相关系数：

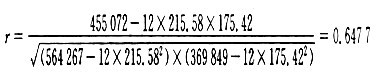
根据前述的判断标准，可以判断x与y之间是显著相关状态。因此，可建立回归直线方程：y=a+bx

根据以上计算可得出线性回归方程为：

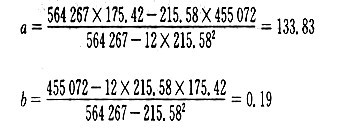
y = 133. 83 + 0.19x

如果该车间2012年第一季度的设备工作时间预计分别为248小时、256小时、 263小时，则各月份的设备维修成本可预测如下：

1月份维修成本预测值=133.83+0.19×248=180. 95（元）

2月份维修成本预测值=133.83+0.19×256=182. 47（元）

3月份维修成本预测值=133.83+0.19×263=183. 80（元）

2.多元线性回归预测法

当影响因变量^变动的因素不止一个时，就必须采用多元线性回归模式对未来的状态进行预测。在此，我们仅讨论二元线性回归模式。 二元回归方程的标准方程为：

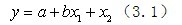
式中 y为因变量，x1和x2为自变量，a、b、c为回归系数。先以总和（∑）的形式表达（3.1）式中的每一项，得出：