由于货币随时间的延续而增值,不同时间单位货币的价值不相等,所以,不同时间的货币收入不宜直接进行比较,需要把他们换算到相同的时间基础上,然后才能进行大小的比较和比率的计算。由于货币随时间的增长过程与复利的计算过程在数学上相似,因此,在换算时广泛使用复利计算的各种方法。
一、现值和终值的计算
终值又称将来值,是现在一定量的资金折算到未来某一时点所对应的金额,通常记作F。现值是指未来某一时点上的资金折算到现在所对应的金额,通常记作P。
现值和终值是一定量资金在前后两个不同时点上对应的价值,其差额即为资金的时间价值。现实生活中计算利息时所称本金、本利的概念相当于资金时间价值理论中的现值和终值,利率(用i表示)可视为资金时间价值的一种具体表现;现值和终值对应的时点之间可以划分为n期(n≥1), 相当于计息期。
为方便计算,本章假定有关字母的含义如下:I为利息;F为终值;P为现值;i为利率(折现率);n为计算利息的期数。
(一)单利的现值和终值
1、单利现值
P=F/(1+n×i)
式中,1/(1+n×i) 为单利现值系数。
【例2-1】某人为了5年后能从银行取出500元,在年利率2%的情况下,目前应存入银行的金额是多少?
解答:P=F/(1+ n×i)=500/(1+5×2%)≈454.55(元)
2、单利终值
F=P(1+ n×i)
式中,(1+n×i) 为单利终值系数。
【例2-2】某人将100元存入银行,年利率2%,求5年后的终值。
解答:F=P(1+ n×i)=100×(1+5×2%)=110(元)
结论:(1)单利的终值和单利的现值互为逆运算;
(2)单利终值系数(1+n×i)和单利现值系数1/(1+n×i)互为倒数。
(二)复利的现值和终值
复利计算方法是指每经过一个计息期,要将该期所派生的利息加入本金再计算利息,逐期滚动计算,俗称“利滚利”。
1、复利现值
P=F/(1+i)n
式中,![]() 为复利现值系数,记作(P/F,I,n);n为计息期。
为复利现值系数,记作(P/F,I,n);n为计息期。
【例2-3】某人为了5年后能从银行取出500元,在复利年利率2%的情况下,目前应存入银行的金额是多少?
解答:P=F/(1+ n×i)n=100/(1+2%)5=90.57
2、复利终值
F=P(1+ i)2
式中,(1+i)n为复利终值系数,记作(F/P,i,n);n为计息期。
【例2-4】某人将100元存入银行,复利年利率2%,求5年后的终值。
解答:F=P(1+ i)n=100×(1+2%)5=110.4(元)
结论:(1)复利终值和复利现值互为逆运算;
(2)复利终值系数(1+i)n和复利现值系数1/(1+i)n互为倒数。
二、年金终值和年金现值的计算
年金是指在相同的时间内以相等的金额收付的系列款项,通常以A表示。年金的形式多种多样,如折旧、租金、利息、保险金、养老金、等额分期收款、等额分期付款、零存整取或整存零取储蓄等通常都采取年金的形式。
年金按其每次收付发生的时点不同,可分为普通年、即付年金、递延年金、永续年金等几种。每期期末收款付的年金,称为普通年金或后付年金;每期期初收付的年金,称为即付年金或预付年金或先付年金;距今若干期以后发生的每期期末收付的年金,称为递延年金;无限期连续收付的年金,称为永续年金。
1、普通年金终值的计算(已知年金A,求终值F)
根据复利现值的方法计算年金终值的公式为:
F=A+A(1+i)+A(1+i)2+A(1+i)3+……+A(1+i)n-1
将两边同时乘以(1+i)得:
F(1+i)=A(1+i)+A(1+i)2+A(1+i)3+A(1+i)4……+A(1+i)n
两式相减得:
F×i=A(1+i)n-A=A×[(1+i)n-1]
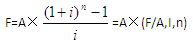
式中,![]()
称为“年金终值系数”,记作(F/A,I,n),可直接查阅“年金终值系数表”。
【例2-5】小王是位热心于公益事业的人,自2002年12月底开始,他每年都要向一位失学儿童捐款。小王向这位失学儿童每年捐款1000元,帮助这位失学儿童从小学一年级读完九年义务教育。假设每年定期存款利率都是2%,则小王9年的捐款在2010年底相当于多少钱?
解答:F=A[(1+i)-1]/i
=1000×[(1+2%)9-1]/2%
=9754.6(元)
或:F=1000×(F/A,2%,9)=1000×9.7546=9754.6(元)
2、偿债基金的计算(已知终值F,求年金A)
偿债基金是指为了在约定的未来某一时点清偿某笔债务或积累一定数额的资金而必须分次等额形成的存款准备金。也就是为使年金终值达到既定金额的年金数额,在普通年金终值公式中解出A,这个A就是偿债基金。![]()
式中![]() ,称为“偿债基金系数”,记作(A/F,I,n)。
,称为“偿债基金系数”,记作(A/F,I,n)。
【例2-6】某人拟在5年后还清10000元债务,从现在起每年年末等额存入银行一笔款项。假设银行利率为10%,则每年需存入多少元?
解答:根据公式
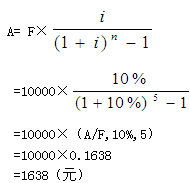
结论:(1)偿债基金和普通年金终值互为逆运算;
(2)偿债基金系数![]() 和普通年金终值系数
和普通年金终值系数![]() 互为倒数。
互为倒数。
3、普通年金现值的计算(已知年金A,求普通年金现值P)
根据复利现值的方法计算年金现值的公式为:
P=A(1+i)-1+A(1+i)-2+ A(1+i)-3+……+A(1+i)-n
将两边同时乘以(1+i)得:
P(1+i)=A(1+i)+ A(1+i)-1+A(1+i)-2+……+A(1+i)-(n-1)
两者相减得:
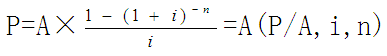
式中,![]()
称为“年金现值系数”,记作(P/A,i,n),可直接查阅“年金现值系数表”。
【例2-7】某投资项目于2010年年初动工,设当年投产,从投产之日起每年可得收益40000元。按年利率6%计算,计算预期10年收益的现值。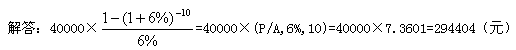
4、年资本回收额的计算(已知普通年金现值P,求年金A)
年资本回收额是指在约定年限内等额回收初始投入资本或清偿所欠债务的金额。
![]()

【例2-8】某企业借得1000万的贷款,在10年以内年利率12%等额偿还,则每年应付的金额是多少?
解答:
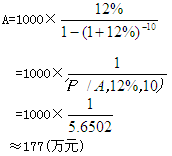
结论:(1)年资本回收额与普通年金现值互为逆运算;
(2)资金回收系数与普通年金现值系数互为倒数。
5、即付年金终值的计算
即付年金终值是指把即付年金每个等额A都换算成第n期期末的数值,再来求和。即付年金终值的计算公司为:
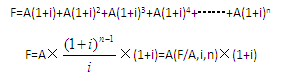
或F=A[(F/A,i,n+1)-1]
【例2-9】为给孩子上大学准备资金,王先生连续6年于每年年初存入银行3000元。若银行存款利率为5%,则王先生在第6年年末能一次取出本利和多少钱?
解答:F=A[(F/A,in+1)-1]
=3000×[(F/A,5%,7)-1]
=3000×(8.1420-1)
=21426(元)
6、即付年金现值的计算
即付年金现值就是吧即付年金每个等额的A都换算成第一期期初的数值即第0期期末的数值,再求和。即付年金现值的计算就是已知每期期初等额收付的年金A,求现值P。
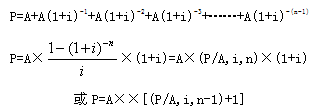
【例2-10】张先生采用分期付款方式购入商品房一套,每年年初付款15000元,分10年付清。若银行利率为6%,该项分期付款相当于一次现金支付的购买价是多少?
解答:P=A×[(P/A,i,n-1)+1]
=15000×[(P/A,6%,9)+1]
=15000×(6.8017+1)
=117025.5(元)
7、递延年金现值的计算
递延年金是指第一次支付发生在第二期或第二期以后的年金。递延年金的支付形式如图2-1所示。从图中可以看出:前三期没有发生支付,一般用m表示递延期数,本例的m=3;第一次支付在第四期期末,连续支付4次,即n=4。
m=3 i=10% n=4 A=100
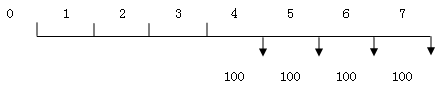
递延年金终值的计算方法和普通年金终值类似,只是要注意期数。
F=A×(F/A,i,n)
=100×(F/A,10%,4)
=100×4.641
=464.1(元)
递延年金现值的计算方法有两种:
第一种方法:
先将递延年金视为n期普通年金,求出在m期普通年金现值,然后再折算到第一期期初。
P0=A×(P/A,i,n)×(P/F,i,m)
第二种方法:
先计算m+n期年金现值,再减去m期年金现值:
P0=A×[(P/A,i,m+n)-(P/A,i,m)]
【例2-11】某企业向银行借入一笔款项,银行贷款的年利率为10%,每年复利一次。银行规定前10年不用还本付息,但从第11年至第20年每年年末偿还本息5000元。
要求:用两种方法计算这笔款项的现值。
解答:
方法一:
P=A×(P/A,i,n)×(P/F,i,m)
=A×(P/A,10%,10)×(P/F,10%,10)
=5000×6.145×0.386
=11860(元)
方法二:
P=A×[(P/A,i,m+n)-(P/A,i,m)]
=A×[(P/A,10%,20)-(P/A,10%,10)]
=5000×(8.514-6.145)
=11845(元)
两种计算方法相差15元,是因小数点的尾数造成的。
8、永续年金现值的计算
无限期定额支付的年金,称为永续年金。
永续年金没有终止的时间,也就没有终值。
永续年金的现值可以看成是一个n无穷大后付年金的现值,则永续年金现值计算如下:
P(n→∞)=A×[1-(1+i)-n]/i=A/i
当n趋向无穷大时,因此,P(n→∞)=A×[1-(1+i)-n]/i趋向A/i。
【例2-12】拟建立一项永久性奖学金,每年计划颁发10000元奖金。若利率为10%,现在应存入多少钱?
解答:P=A/i=10000/10%=100000(元)
