在细节测试中进行审计抽样，可能使用统计抽样，也可能使用非统计抽样。两种抽样方法的基本流程和主要步骤相同，但在部分环节所用的具体方法有所差别。以下分述之。

一、在细节测试中使用非统计抽样方法

（一）样本设计阶段

实施细节测试时，注册会计师在样本设计阶段必须完成的工作包括四个环节：确定测试目标、定义总体、定义抽样单元，界定错报。

1．明确测试目标

在细节测试中，抽样通常用来为有关财务报表金额的一项或多项认定提供特定水平的合理保证（如应收账款的存在性）。因而细节测试旨在对各类交易、账户余额、列报的相关认定进行测试，尤其是对存在或发生、计价认定的测试。注册会计师实施审计程序的目标就是确定相关认定是否存在重大错报。通过在账户余额中选取项目进行测试，注册会计师可以检查出那些虚构项目、余额中不应包含的项目（分类错误的项目）以及估价错误的项目。

2．定义总体

(1)考虑总体的适当性和完整性。注册会计师应确信抽样总体适合于特定的审计目标。例如，注册会计师如果对已记录的项目进行抽样，就无法发现由于某些项目被隐瞒而导致的金额低估。为发现这类低估错报，注册会计师应从包含被隐瞒项目的来源选取样本。例如，注册会计师可能对随后的现金支付进行抽样，以测试由隐瞒采购所导致的应付账款账面金额低估；或者对装运单据进行抽样，以发现由已装运但未确认为销售的交易所导致的低估销售收入问题。

注册会计师实际上是从代表总体的实物中选取样本项目。如果注册会计师将总体定义为特定日期的所有应收账款余额，那么代表总体的实物则可能就是该日的应收账款明细账。注册会计师要考虑代表总体的实物是否包括了所有总体项目。

(2)识别单个重大项目（超过可容忍错报应该单独测试的项目）和极不重要的项目。在细节测试中计划抽样时，注册会计师应当运用职业判断，判断某账户余额或交易类型中是否存在及存在哪些应该单独测试而不能放在抽样总体中的项目。某一项目可能由于存在特别风险或者金额较大而应被视为单个重大项目。注册会计师应当对单个重大项目逐一实施检查，以将抽样风险控制在合理的范围内。单个重大项目包括那些潜在错报可能超过可容忍错报的所有单个项目，以及异常的余额或交易。注册会计师进行单独测试的所有项目都不构成抽样总体。增加单独测试的账户可以减少样本规模。因此单独测试的账户越多，拟抽样的剩余总体越小，可容忍错报占抽样总体的比例越高。

如果主要关注高估，注册会计师会发现总体中有些项目加总起来是不重要的，或者被认为代表较低的固有风险，可以从抽样计划中剔除这些项目，以集中精力于与审计相关度更高的项目，必要时可以对固有风险很低的项目实施分析程序。

3．定义抽样单元

在细节测试中，注册会计师应根据审计目标和所实施审计程序的性质，定义抽样单元。抽样单元可能是一个账户余额、一笔交易或交易中的一个记录（如销售发票中的单个项目），甚至是每个货币单元。例如，如果抽样的目标是测试应收账款是否存在，注册会计师可能选择各应收账款明细账余额、发票或发票上的单个项目作为抽样单元。选择的标准是，如何定义抽样单元能使审计抽样实现最佳的效率和效果。

注册会计师定义抽样单元时也应考虑实施计划的审计程序或替代程序的难易程度。如果将抽样单元界定为客户明细账余额，当某客户没有回函证实该余额时，注册会计师可能需要对构成该余额的每一笔交易进行测试。因此，如果将抽样单元界定为构成应收账款余额的每笔交易，审计抽样的效率可能更高。

4．界定错报

在细节测试中，误差是指错报，注册会计师应根据审计目标，确定什么构成错报。例如，在对应收账款存在性的细节测试中（如函证），客户在函证日之前支付、被审计单位在函证日之后不久收到的款项不构成误差。而且，被审计单位在不同客户之间误登明细账也不影响应收账款总账余额。即使在不同客户之间误登明细账可能对审计的其他方面（如对舞弊的可能性或坏账准备的适当性的评估）产生重要影响，注册会计师在评价应收账款函证程序的样本结果时不宜将其判定为误差。在审计抽样中，注册会计师应根据审计目标界定错报。如果错报定义为账面金额与注册会计师审定金额之间的差异，不符合相关特征的差异就不是错报。例如，在登记明细账时发生的差错如果不导致账户余额合计数发生错误，就不属于错报。注册会计师还可能将被审计单位自己发现并已在适当期间予以更正的错报排除在外。

（二）选取样本阶段

1．确定样本规模

(l)影响样本规模的因素。如果在细节测试中使用非统计抽样，注册会计师在确定适当的样本规模时，也需要考虑相关的影响因素，如总体变异性，可接受抽样风险，可容忍错报，预计总体错报，以及总体规模等，即使注册会计师无法明确地量化这些因素。

①总体的变异性。总体项目的某一特征（如金额）经常存在重大的变异性。在细节测试中确定适当的样本规模时，注册会计师应考虑特征的变异性。注册会计师通常根据项目账面金额的变异性估计总体项目审定金额的变异性。衡量这种变异或分散程度的指标是标准差。注册会计师在使用非统计抽样时，不需量化期望的总体标准差，但要用“大”或“小”等定性指标来估计总体的变异性。总体项目的变异性越低，通常样本规模越小。

②可接受的抽样风险。细节测试中的抽样风险分为两类：误受风险和误拒风险。在细节测试中使用非统计抽样方法时，注册会计师主要关注误受风险。

在确定可接受的误受风险水平时，注册会计师需要考虑下列因素：

a．注册会计师愿意接受的审计风险水平；

b．评估的重大错报风险水平；

c．针对同一审计目标（财务报表认定）的其他实质性程序的检查风险，包括分析程序。

在实务中，注册会计师愿意承担的审计风险通常为5%～10%。当审计风险既定时，如果注册会计师将重大错报风险评估为低水平，就可以在实质性程序中接受较高的误受风险。当可接受的误受风险增加时，实质性程序所需的样本规模降低。相反，如果注册会计师评估的重大错报风险水平较高，可接受的误受风险降低，所需的样本规模就增加。

注册会计师对其他实质性程序的依赖程度对样本规模的影响与此类似，其他实质性程序包括与同一审计目标相关的分析程序。

在细节测试中，误拒风险与审计的效率有关，如果注册会计师决定接受一个较高的误拒风险，所需的样本规模降低。在设计样本时，与控制测试中对信赖不足风险的关注相比，注册会计师在细节测试中对误拒风险的关注程度通常更高。如果控制测试中的样本结果不支持计划的重大错报风险评估水平，注册会计师可以实施其他的控制测试以支持计划的重大错报风险评估水平，或根据测试结果提高重大错报风险评估水平。由于替代审计程序比较容易获得，因此，对控制信赖不足给注册会计师和被审计单位造成的不便通常相对较小。但是，如果在某类交易或账户余额的账面金额可能不存在重大错报时根据样本结果得出存在重大错报的结论，注册会计师采用替代方法可能花费的成本大得多。通常，注册会计师需要与被审计单位的人员进一步讨论，并实施额外的审计程序。

③可容忍错报。可容忍错报与注册会计师计划的重要性水平有关。某账户的可容忍错报实际上就是该账户的重要性水平。对特定的账户余额或交易类型而言，当误受风险一定时，如果注册会计师确定的可容忍错报降低，为实现审计目标所需的样本规模就增加。

④预计总体错报。在确定细节测试所需的样本规模时，注册会计师还需要考虑预计在账户余额或交易中存在的错报金额和频率。预计总体错报的规模或频率降低，所需的样本规模也降低。相反，预计总体错报的规模或频率增加，所需的样本规模也增加。

注册会计师在运用职业判断确定预计错报额时，应当考虑被审计单位的经营状况，以前年度对账户余额或交易类型进行测试的结果，初始样本的结果，相关实质性程序的结果，以及相关控制测试的结果等因素。

⑤总体规模。总体中的项目数量在细节测试中对样本规模的影响很小。因此，按总体的固定百分比确定样本规模通常缺乏效率。

(2)利用模型确定样本规模。注册会计师在细节测试中可以用来确定样

本规模的模型如下：

本模型只用于说明计划抽样时考虑的各种因素对样本规模的影响，它不能代替职业判断。注册会计师使用本模型时，需要在下列方面运用职业判断：

①评估重大错报风险；

②确定可容忍错报；

③估计预计总体错报；

④评估其他实质性程序未能发现重大错报的风险；

⑤剔除百分之百检查的项目后估计总体的账面金额；

⑥调整确定样本规模。

对本模型计算的样本规模进行适当调整后，注册会计师可以确定非统计抽样所需的适当样本规模。注册会计师应考虑到，本模型基于具有高度统计效率和高度分层的抽样方法，因此应根据非统计抽样中分层程度等因素对本表确定的样本规模进行调整，以体现非统计抽样方法和本表使用的统计抽样方法的差异。

使用本模型时确定样本规模的步骤如下：

①考虑重大错报风险，将其评估为最高、高、中和低四个等级；

②确定可容忍错报；

③评估用于测试相同认定的其他实质性程序（如分析程序）未能发现该认定中重大错报的风险；

a.最高——没有实施其他实质性程序测试相同认定

b．高——预计用于测试相同认定的其他实质性程序不能有效地发现该认定中的重大错报

c．中——预计用于测试相同认定的其他实质性程序发现该认定中重大错报的有效程度适中

d．低——预计用于测试相同认定的其他实质性程序能有效地发现该认定中的重大错报

④剔除百分之百检查的所有项目后估计总体的账面金额；

⑤从表10—13中选择适当的保证系数，并适用下列公式估计样本规模：

表10—13保证系数表

评估的重大错报风险	其他实质性程序未能发现重大错报风险
	最高	高	中	低
最高	3.00	2.7	2.30	2.00
高	2.70	2.4	2.00	1.60
中	2.30	2.1	1.60	1.20
低	2.00	1.6	1.20	1.00

⑥调整估计的样本规模，以反映非统计方法与本模型使用的统计方法在效率上的差异。在实务中，如果样本不是以统计有效的方式选取，注册会计师调整样本规模的幅度通常在10%—50%。

 2．选取样本并对其实施审计程序

在非统计抽样方法中，注册会计师可以使用随机数表或计算机辅助审计技术选样、系统选样，也可以使用随意选样。注册会计师应当仔细选取样本，以使样本能够代表抽样总体的特征。在选取样本之前，注册会计师通常先识别单个重大项目。然后，从剩余项目中选取样本，或者对剩余项目分层，并将样本规模相应分配给各层。注册会计师从每一层中选取样本，但选取的方法应当能使样本具有代表性。注册会计师应对选取的每一个样本实施计划的审计程序。

分层使具有相同特征的个体样本被包含在一个层中，从而降低了样本个体的可变性，同时，对于既定的抽样风险，样本规模能够最小化。因此，必须对总体分层进行评估，否则可能会因为样本太小而不能有效控制抽样风险。利用总体金额来评估是否应对总体进行分层的方法通常非常简便。为了进行评估，注册会计师通常应按照金额升序或降序的方式对总体项目进行排序，将总体分为金额大约相等的两个部分。如果各部分中存在明显不成比例的项目数，那么应对其进行分层。

例如，审计抽样的总体为22 000000元，含1 500个项目，被分为11 200 000元和10 800 000元两个大约金额相等的部分。如果两部分分别有300个和1 200个项目，则须对其进行分层。如果一个含有项目数为570个，而另一个为630个，那么不必要分层。

如果总体还需要分层，那么注册会计师也可能考虑用三层对总体进行评估。评估的过程仍然相同，只是需要把金额分成大约相同的三部分。如果三个部分中的项目数量明显不成比例，则应使用三层而不是两层。对于大多数审计，没有必要分三层以上。

（三）评价样本结果阶段

1．考虑错报的性质和原因

除了评价错报的频率和金额之外，注册会计师还要对错报进行定性分析，分析错报的性质和原因，判断其对财务报表重大错报的影响。

2．推断总体错报

当实施细节测试时，注册会计师应当根据样本中发现的错报推断总体错报。在非统计抽样中，根据样本中发现的错报金额推断总体错报金额的方法有多种，注册会计师可以从中选择其一。本节介绍两种常用的方法。

第一种方法是比率法，即用样本中的错报金额除以该样本中包含的账面金额占总体账面总金额的比例。例如，注册会计师选取的样本可能包含了应收账款账户账面金额的10%。如果注册会计师在样本中发现了100元的错报，其对总体错报的最佳估计为1 000元（100元÷10%）。这种方法不需使用总体规模。比率估计法在错报金额与抽样单元金额相关时最为适用，是大多数审计抽样中注册会计师首选的总体推断方法。

第二种方法是差异法，即计算样本中所有项目审定金额和账面金额的平均差异，并推断至总体的全部项目。例如，注册会计师选取的非统计抽样样本为100个项目。如果注册会计师在样本中发现的错报为200元，样本项目审定金额和账面金额的平均差异则为2元（200元÷100）。然后注册会计师可以用总体规模（本例中为5 000）乘以样本项目的平均差异2元，以估计总体的错报金额。注册会计师估计的总体错报则为10 000元（5 000 x2元）。差异估计法通常更适用于错报金额与抽样单元本身而不是与其金额相关的情况。

如果注册会计师在设计样本时将进行抽样的项目分为几组，则要在每组分别推断错报，然后将各组推断的金额加总，计算估计总体错报。注册会计师还要将在进行百分之百检查的个别重大项目中发现的所有错报与推断的错报金额汇总。

3．考虑抽样风险并得出总体结论

注册会计师应当将推断的总体错报额与百分之百检查的项目中所发现的错报加总，并要求被审计单位调整已经发现的错报。依据被审计单位已更正的错报对推断的总体错报额进行调整后，注册会计师要将其与该类交易或账户余额的可容忍错报相比较，并适当考虑抽样风险，以评价样本结果。如果推断的错报总额低于账户余额或交易类型的可容忍错报，注册会计师要考虑即使总体的实际错报金额超过可容忍错报，仍可能出现这一情况的风险。例如，如果1 000 000元的某账户余额的可容忍错报为50 000元，根据适当的样本推断的总体错报为10 000元，由于推断的总体错报远远低于可容忍错报，注册会计师可能合理确信，总体实际错报金额超过可容忍错报的抽样风险很低，因而可以接受。另外，如果推断的错报总额接近或超过可容忍错报，注册会计师通常得出总体实际错报超过可容忍错报的结论。

在非统计抽样中，注册会计师运用其经验和职业判断进行这种评价。但是，当推断的错报与可容忍错报的差距既不很小又不很大时，注册会计师应当仔细考虑，实际错报超过可容忍错报的风险是否高得无法接受。

如果样本结果不支持总体账面金额，且注册会计师认为账面金额可能存在错报，注册会计师在评价财务报表整体是否存在重大错报时，应当将错报与其他审计证据一起考虑。通常，注册会计师会建议被审计单位对错报进行调查，且在必要时调整账面记录。

（四）记录抽样程序

注册会计师要记录所实施的审计程序，以形成审计工作底稿。在实质性程序中使用审计抽样时，注册会计师通常记录下列内容：

(1)测试目标和对与此目标相关的其他审计程序的描述；

(2)总体和抽样单元的定义，包括注册会计师如何确定总体的完整性；

(3)错报的定义；

(4)误受风险、误拒风险和可容忍错报；

(5)使用的审计抽样方法；

(6)选样方法；

(7)描述抽样程序的实施，以及样本中发现的错报清单；

(8)对样本的评价和总体结论摘要。

对样本的评价和总体结论摘要可能包含根据样本中发现的错报推断总体，对注册会计师如何考虑抽样风险的解释，以及关于总体的最终结论。工作底稿也可记录注册会计师对错报的性质方面的考虑。

（五）非统计抽样示例

假设××会计师事务所的注册会计师拟通过函证测试ABC公司20 x8年12月31日应收账款余额的存在认定。ABC公司当年12月31日应收账款账户剔除贷方余额账户和零余额账户后的借方余额共计2 410 000元，由l651个借方账户组成。

注册会计师初步确定的被审计单位财务报表层次重要性水平为280 000元。注册会计师以此为基础，根据被审计单位特点、风险评估结果和内部控制运行有效性等因素，确定可容忍错报水平为140 000元。

注册会计师将总体定义为20 x8年12月31日剔除贷方余额账户和零余额账户以及剔除单个重大项目和极不重要项目之后的应收账款余额，代表总体的实物是20 x8年12月31日剔除单个重大项目和极不重要项目之后的应收账款借方余额明细账账户。注册会计师定义的抽样单元是每个应收账款明细账账户。

注册会计师将重大项目定义为账面金额在140 000元以上的所有应收账款明细账账户，并决定对其进行单独测试；将极不重要项目定义为账面金额在1 000元以下的所有应收账款明细账账户，并决定对其不实施审计程序。剔除重大项目和极不重要项目后抽样总体变成2 200 000元，包括l500个账户，如表10—14所示。

表10—14 抽样总体

项目分类	项目数量	金额（元）
重大项目	1	200 000
极不重要项目	150	10 000
抽样总体	1 500	2 200 000
合计	1 651	2 410 000

注册会计师将错报界定为被审计单位不能合理解释并提供相应依据的、应收账款账面金额与注册会计师实施抽样所获得的审计证据所支持的金额之间的差异（高估）。错报不包括明细账户之间的误记、在途款项，以及被审计单位已经修改的差异。

注册会计师将应收账款存在认定的重大错报风险水平评估为“中”，且由于没有对应收账款的存在认定实施与函证目标相同的其他实质性程序而将“其他实质性程序的检查风险”评估为“最高”。根据表10 - 13得到的保证系数为2.3。

注册会计师根据下列公式估计样本规模：

2 400 000÷140 000×2.3=36

注册会计师将抽样总体分成金额大致相等的两层，发现两层分别包含的项目数量相差很大，因此决定分层。注册会计师将36个样本平均分配到这两个账面金额大致相等的层，每层18个样本。因此，注册会计师从第一层300个账户中选取18个，从第二层1 200个账户中也选取18个。样本分层情况如表10—15所示。

表10—15样本分层表

层	层账面金额（元）	层账面数量（个）	层样本规模（个）
第1层	1 120 000	300	18
第2层	1 080 000	1 200	18
合计	2 200 000	1 500	36

注册会计师向37个客户寄发了询证函，包括1个重大项目和36个选出的样本。重大项目中存在的错报为1 034元。36个样本中发现的错报如表10—16所示。

表10—16   样本错报汇总表

层	层样本账面总额（元）	层样本错报额（元）	层样本错报数量（元）	层错报额（元）
第1层	124 900	2 4100	2	21 521
第2层	30 500	550	1	19 475
合计	155 400	2 950	3	40 996

注：层错报额=层样本错报额÷层样本账面总额×层账面总额。

注册会计师利用比率法推断的总体错报额为40 996元，加上重大项目中发现的错报1 034元，计算出错报总额为42 030元。注册会计师将推断的错报总额42 030元与可容忍错报140 000元比较，认为应收账款借方账面余额发生的错报超过可容忍错报的风险很小，因此总体可以接受。也就是说，即使在其推断的错报上加上合理的抽样风险允许限度，也不会出现一个超过可容忍错报的总额。注册会计师调查了错报的性质和原因，确定它们是由笔误所导致的，因此不代表额外的审计风险。

注册会计师得出结论，样本结果支持应收账款账面余额。但是，注册会计师还应将根据样本结果推断的错报与其他已知和可能的错报汇总，以评价财务报表整体是否可能存在重大错报。

二、在细节测试中使用统计抽样

统计抽样和非统计抽样的流程和步骤完全一样，只是在确定样本规模、选取样本和推断总体的具体方法上有所差别。注册会计师在细节测试中使用的统计抽样方法主要包括传统变量抽样和概率比例规模抽样法（以下简称PPS抽样）。两种统计抽样方法的区别主要体现在确定样本规模和推断总体两个方面。

（一）传统变量抽样

传统变量抽样在确定样本规模时需要量化可接受的抽样风险、可容忍错报、预计总体错报等影响因素，并代人专门的统计公式中计算所需的样本数量。根据推断总体的方法不同，传统变量抽样又可以分为三种具体的方法：均值估计抽样、差额估计抽样和比率估计抽样。

1．均值估计抽样。均值估计抽样是指通过抽样审查确定样本的平均值，再根据样本平均值推断总体的平均值和总值的一种变量抽样方法。使用这种方法时，注册会计师先计算样本中所有项目审定金额的平均值，然后用这个样本平均值乘以总体规模，得出总体金额的估计值。总体估计金额和总体账面金额之间的差额就是推断的总体错报。例如，注册会计师从总体规模为1 000、账面金额为1 000 000元的存货项目中选择了200个项目作为样本。在确定了正确的采购价格并重新计算了价格与数量的乘积之后，注册会计师将200个样本项目的审定金额加总后除以200，确定样本项目的平均审定金额为980元。然后计算估计的存货余额为980 000元(980×1 000)。推断的总体错报就是20 000元(1 000 000 -980 000)。

2．差额估计抽样。差额估计抽样是以样本实际金额与账面金额的平均差额来估计总体实际金额与账面金额的平均差额，然后再以这个平均差额乘以总体规模，从而求出总体的实际金额与账面金额的差额（即总体错报）的一种方法。差额估计抽样的计算公式如下：

推断的总体错报=平均错报×总体规模

使用这种方法时，注册会计师先计算样本项目的平均错报，然后根据这个样本平均错报推断总体。例如，注册会计师从总体规模为1000的存货项目中选取了200个项目进行检查。总体的账面金额总额为1040000元。注册会计师逐一比较200个样本项目的审定金额和账面金额并将账面金额（208000元）和审定金额（196000元）之间的差异加总，本例中为12000元。12000元的差额除以样本项目个数200，得到样本平均错报60元。然后注册会计师用这个平均错报乘以总体规模，计算出总体错报为60000元（60元×1000）。

3.比率估计抽样。比率估计抽样是指以样本的实际金额与账面金额之间的比率关系来估计总体实际金额与账面金额之间的比率关系，然后再以这个比率去乘总体的账面金额，从而求出估计的总体实际金额的一种抽样方法。比率估计抽样法的计算公式如下：

估计的总体实际金额=总体账面金额×比率

推断的总体错报=估计的总体实际金额-总体账面金额

如果上例中注册会计师使用比率估计抽样，样本审定金额合计与样本账面金额的比例则为0.94(196 000÷208 000)。注册会计师用总体的账面金额乘以该比例0.94，得到估计的存货余额977 600元(1 040 000×0.94)。推断的总体错报则为62 400元(1 040 000 -977 600)。

如果未对总体进行分层，注册会计师通常不使用均值估计抽样，因为此时所需的样本规模可能太大，以至于对一般的审计而言不符合成本效益原则。比率估计抽样和差额估计抽样都要求样本项目存在错报。如果样本项目的审定金额和账面金额之间没有差异，这两种方法使用的公式所隐含的机理就会导致错误的结论。如果注册会计师决定使用统计抽样，且预计只发现少量差异，就不应使用比率估计抽样和差额估计抽样，而应考虑使用其他的替代方法，如均值估计抽样或PPS抽样。

设计传统变量抽样所需的数学计算，包括样本规模的计算，对于手工应用来说显得复杂且困难。注册会计师在使用传统变量抽样时通常运用计算机程序确定样本规模，一般不需懂得这些方法所用的数学公式。注册会计师在确定样本规模时要考虑可容忍错报和误受风险，有时也需要考虑误拒风险。

下面以XYZ公司审计中的积极函证为例，来说明差额估计抽样的运用。XYZ公司的背景资料如下：在账龄试算表中总共列示了4 000笔应收账款，账面价值合计为600 000元。注册会计师认为该公司的内部控制存在薄弱环节，并预期审计中还将会在账面金额中发现大量的小额错报。其总资产为2 500 000元，税前净收益为400 000元。由于财务报表的使用者有限，并且XYZ公司的财务状况良好，因此可接受的审计风险较高，分析程序的结果表明没有重大问题。在整个讨论过程中，均假定所有的函证都有答复或都已执行了有效的替代程序。因此，样本规模就是寄出的积极函证的数量。

注册会计师对XYZ公司进行审计测试的目标是确定在考虑坏账准备之前的应收账款是否存在重要错报。由于应收账款数目较大，决定采用审计抽样。XYZ公司应收账款的总体容量为4 000笔。注册会计师确定的可容忍错报额为21 000元。

在XYZ公司应收账款审计中，注册会计师要确定两类风险：

一类是可接受的误受风险，是指在应收账款实际错报额超过21 000元时，认为应收账款金额正确的风险。它受可接受的审计风险、控制测试和交易实质性程序的结果、分析程序和应收账款在财务报表中的相对重要性等方面的影响。在XYZ公司审计中，采用10%的可接受的误受风险。

另一类是可接受的误拒风险，是在应收账款实际上没有发生重要错报时，注册会计师认为应收账款不正确而拒绝接受的风险。它要受重新抽样所要追加的成本影响。由于进行第二次函证的成本很高，因此采用25%的可接受的误拒风险。对于那些增加样本规模的成本不是很高的审计测试，通常采用较高的可接受的误拒风险。

注册会计师根据以前年度的审计测试结果，确定XYZ公司的预计总体错报为1 500元（高估）。

由于在确定初始样本规模时，需要预先估计总体中个别错报的变动程度，它是以总体标准差来衡量的，因此注册会计师根据以前年度的审计测试结果，估计XYZ公司的总体标准差为20元。

现在，XYZ公司的初始样本规模可用下列公式计算：

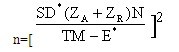
将该公式应用于XYZ公司，得：

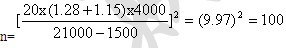
表10 -17置信度、可接受的误受风险、可接受的误拒风险的置信系数表

信度（%）	可接受的误受风险（%）	可接受的误拒风险（%）	置信系数
99	0.5	l	2.58
95	2.5	5	1.96
90	5	10	1.64
80	10	20	1.28
75	12.5	25	1.15
70	15	30	1.04
60	20	40	0.84
50	25	50	0.67
40	30	60	0.52
30	35	70	O.39
20	40	80	0.25
10	45	90	0.13
O	50	100	O

注册会计师运用前面所讨论的选样方法之一随机选取了100个样本项目进行函证。表10—18列示了注册会计师计算总体错报上限的过程。

表10—18  总体错报界限的计算表

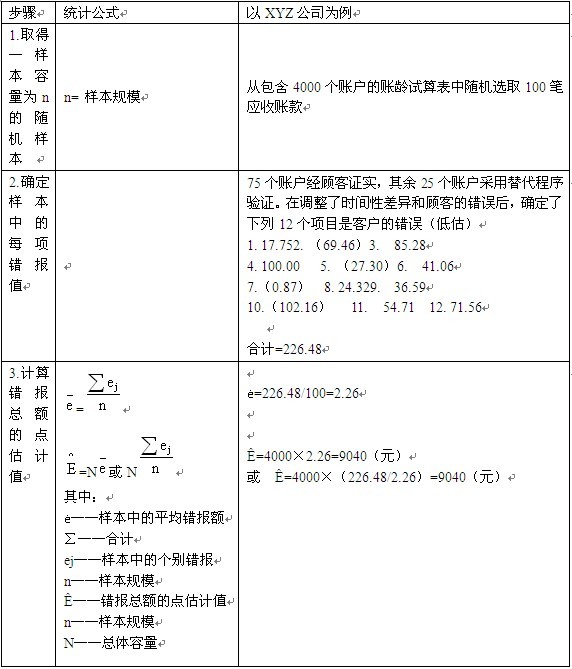
计算的总体错报界限等于错报总额的点估计值加减抽样风险允许限度。在本例中，计算的总体错报上限为19 840元，表示总体高估超过19 840元的风险是10%，计算的总体错报下限为-1 760元，表示总体低估超过1 760元的风险是10%。由于错报的双边置信区间完全落入了正负可容忍错报范围内，那么账面价值没有重大错报的假设就可以接受。因此，应收账款的账面价值是可以接受的。

（二）概率比例规模抽样（Probability-proportional-to-size sampling，简称PPS抽样）

细节测试中运用的两种统计抽样方法，即传统变量抽样和PPS抽样，都能为注册会计师实现审计目标提供充分的证据。但在有些情况下，PPS抽样比传统变量抽样更实用。

1．PPS抽样的概念

PPS抽样是一种运用属性抽样原理对货币金额而不是对发生率得出结论的统计抽样方法。PPS抽样以货币单元作为抽样单元，有时也被称为金额加权抽样、货币单元抽样、累计货币金额抽样，以及综合属性变量抽样等。在该方法下总体中的每个货币单元被选中的机会相同，所以总体中某一项目被选中的概率等于该项目的金额与总体金额的比率。项目金额越大，被选中的概率就越大。但实际上注册会计师并不是对总体中的货币单元实施检查，而是对包含被选取货币单元的余额或交易实施检查。注册会计师检查的余额或交易被称为逻辑单元或实物单元。PPS抽样有助于注册会计师将审计重点放在较大的余额或交易。此抽样方法之所以得名，是因为总体中每一余额或交易被选取的概率与其账面金额（规模）成比例。

注册会计师进行PPS抽样必须满足两个条件：第一，总体的错报率很低（低于10%），且总体规模在2 000以上。这是PPS抽样使用的泊松分布的要求。第二，总体中任一项目的错报不能超过该项目的账面金额。这就是说，如果某账户的账面金额是100元，其错报金额不能超过100元。

2．PPS抽样的优缺点

除了具备统计抽样的一般优点之外，PPS抽样还具有一些特殊之处。了解PPS抽样的优点和不足有助于注册会计师确定在测试中是否使用PPS抽样。

PPS抽样的优点包括下列方面：

(l) PPS抽样一般比传统变量抽样更易于使用。由于PPS抽样以属性抽样原理为基础，注册会计师可以很方便地计算样本规模，手工或使用量表评价样本结果。样本的选取可以在计算机程序或计算器的协助下进行。

(2) PPS抽样可以如同大海捞针一样发现极少量的大额错报，原因在于它通过将少量的大额实物单元拆成数量众多、金额很小的货币单元，从而赋予大额项目更多的机会被选人样本。

(3) PPS抽样的样本规模无须考虑被审计金额的预计变异性。传统变量抽样的样本规模是在总体项目共有特征的变异性或标准差的基础上计算的。PPS抽样在确定所需的样本规模时不需要直接考虑货币金额的标准差。

(4) PPS抽样中项目被选取的概率与其货币金额大小成比例，因而生成的样本自动分层。如果使用传统变量抽样，注册会计师通常需要对总体进行分层，以减小样本规模。在PPS抽样中，如果项目金额超过选样间距，PPS系统选样将自动识别所有单个重大项目。

(5)如果注册会计师预计错报不存在或很小，PPS抽样的样本规模通常比传统变量抽样方法更小。

(6) PPS抽样的样本更容易设计，且可在能够获得完整的总体之前开始选取样本。

PPS抽样的缺点包括下列方面：

(1) PPS抽样要求总体每一实物单元的错报金额不能超出其账面金额。

(2)在PPS抽样中，被低估的实物单元被选取的概率更低。PPS抽样不适用于测试低估。如果注册会计师在PPS抽样的样本中发现低估，在评价样本时需要特别考虑。

(3)对零余额或负余额的选取需要在设计时特别考虑。例如，如果准备对应收账款进行抽样，注册会计师可能需要将贷方余额分离出去，作为一个单独的总体。如果检查零余额的项目对审计目标非常重要，注册会计师需要单独对其进行测试，因为零余额在PPS抽样中不会被选取。

(4)当总体中错报数量增加时，PPS抽样所需的样本规模也会增加。在这些情况下，PPS抽样的样本规模可能大于传统变量抽样所需的规模。

(5)当发现错报时，如果风险水平一定，PPS抽样在评价样本时可能高估抽样风险的影响，从而导致注册会计师更可能拒绝一个可接受的总体账面金额。

(6)在PPS抽样中注册会计师通常需要逐个累计总体金额。但如果相关的会计数据以电子形式储存，就不会额外增加大量的审计成本。

3．确定样本规模

(1)公式法

在PPS抽样中，注册会计师根据下列公式计算样本规模：

因此，注册会计师确定样本规模时必须事先确定下列因素：总体账面价值、误受风险的风险系数、可容忍错报、预计总体错报，以及扩张系数。

其中，风险系数代表注册会计师愿意接受的误受风险。PPS抽样中的抽样风险就是指误受风险，注册会计师通过确定抽样计划中使用的抽样风险水平来控制误受风险。在确定可接受的误受风险时，注册会计师需要使用审计风险模型，即：误受风险=审计风险÷（控制风险×分析程序风险）。不同水平的误

受风险对应的风险系数可从表10 -19中查找。根据表10 - 19中“高估错报数量”为0的那一行，即可确定误受风险的风险系数。例如，如果所需的误受风险为10%，注册会计师从表10 - 19中查得的风险系数为2.31。

表10 -19PPS抽样风险系数表（适用于高估）

高估错报数量	1%	5%	10%	15%	误受风险20%	25%	30%	37%	50%
0	4.61	3	2.31	1.9	1.61	1.39	1.21	1	0.7
1	6.64	4.75	3.89	3.38	3	2.7	2.44	2.14	1.68
2	8.41	6.3	5.33	4.72	4.28	3.93	3.62	3.25	2.68
3	10.05	7.76	6.69	6.02	5.52	5.11	4.77	4.34	3.68
4	11.61	9.16	8,00	7.27	6.73	6.28	5.9	5.43	4.68
5	13.11	10.52	9.28	8.5	7.91	7.43	7.01	6.49	5.68
6	14.57	11.85	10.54	9.71	9.08	8.56	8.12	7.56	6.67
7	16	13.15	11.78	10.9	10.24	9.69	9.21	8.63	7.67
8	17.41	14.44	13	12.08	11.38	10.81	10.31	9.68	8.67
9	18.79	15.71	14.21	13.25	12.52	11.92	11.39	10.74	9.67
10	20.15	16.97	15.41	14.42	13.66	13.02	12.47	11.79	10.67
11	21.49	18.21	16.6	15.57	14.78	14.13	13.55	12.84	11.67
12	22.83	19.45	17.79	16.72	15.9	15.22	14.63	13.89	12,67
13	24.14	20.67	18.96	17.86	17.02	16.32	15.7	14.93	13.67
14	25.45	21.89	20.13	19	18.13	17.4	16.77	15.97	14.67
15	26.75	23.1	21.3	20.13	19.24	18.49	17.84	17.02	15.67
16	28.03	24.31	22.46	21.26	20.34	19.58	18.9	18.06	16.67
17	29.31	25.5	23.61	22.39	21.44	20.66	19.97	19.1	17.67
18	30.59	26.7	24.76	23.51	22.54	21.74	21.03	20.14	18.67
19	31.85	27.88	25.91	24.63	23.64	22.81	22.09	21.18	19.67
20	33.11	29.07	27.05	25.74	24.73	23.89	23.15	22.22	20.67

此外，注册会计师通过估计预计总体错报而间接地控制误拒风险。如果注册会计师低估了预计总体错报，样本规模就会太小，从而需要进行额外测试。在PPS抽样中，注册会计师不需要特别控制误拒风险。

如果注册会计师预计总体中存在错报，在使用公式法计算样本规模时必须对可容忍错报进行调整，即从可容忍错报中减去预计错报的影响。预计错报的影响等于预计错报与适当的扩张系数的乘积。下列表10 - 20提供了一些常用的误受风险所对应的扩张系数。例如，如果误受风险为20%，扩张系数就是1.3。

表10 -20预计总体错报的扩张系数表

	1%	5%	10%	15%	误受风险20%	25%	30%	37%	50%
扩张系数	1.9	1.6	1.5	1.4	1.3	1.25	1.2	1.15	1

例如，总体账面价值是500 000元，误受风险是5 010，可容忍错报是25 000元，预计总体错报是6 250元，样本规模就是：

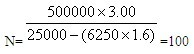
其中，风险系数根据表10 - 19中“高估错报数量为0”确定为3.00。

(2)查表法

由于PPS抽样以属性抽样原理为基础，注册会计师也可以直接使用控制测试的统计抽样样本量表（参见本章第三节）。这比使用扩张系数近似值所计算的样本规模更加准确。注册会计师将可容忍错报和预计总体错报额从绝对数形式转化为相对数形式，即转化为占总体账面金额的百分比，并使用表中相应比例所对应的样本规模。例如，注册会计师为一个账面金额为500 000元的总体设计PPS抽样，且确定的可容忍错报为15 000元，预计总体错报为2 500元。注册会计师计算出可容忍错报占账面金额的比例为3%（15 000元÷500 000元），预计错报占账面金额的比例为0. 5%（2 500÷500 000元）。当可容忍误差率为3%，预计误差率为0.5%时，5%的信赖过度风险对应的样本规模为157个。然后，注册会计师确定选样间距为3 185元（500 000元÷157）。如果注册会计师计算的预计错报比例和可容忍错报比例在表中没有出现，通常用插入法推算所需的样本规模。然后，注册会计师用账面金额除以样本规模计算选样间距。

4．选取样本

(1)简介

PPS抽样是属性抽样的变种，它可以得出关于总体中错报总额的结论。与一般的属性抽样关注实物单元（如发票或收据）不同，PPS抽样关注总体的货币单元。假设注册会计师对一个100 000元的应收账款总体进行抽样，该总体包含5 000个明细账账户。注册会计师将100 000个货币单元视为总体并从中抽取样本，而不是将5 000个不同的实物单元作为总体。另外，PPS抽样以货币单元作为抽样单元，但注册会计师却不是对具体货币单元进行审计，而必须针对实物单元（或称逻辑单元）实施审计测试。货币单元只是起一个类似钩子的作用，从而带出与之相关联的一个实物单元。要找到与被选中的特定货币单元相联系的实物单元，注册会计师必须逐项累计总体中的项目。

例如，在表10 - 21中，注册会计师要在l—7 376（具体金额）之间的总体项目中随机选取样本。但是，为了执行审计程序，注册会计师必须找出l～12（逻辑单元）之间的总体项目。如果注册会计师选取的随机数是3 014，则与该数相联系的逻辑单元就是项目6，因为3 014位于2 963～3 105之间。

这种选样方法导致项目被选取的概率与其规模成正比例。也就是说，金额为100元的项目被选中的机会是金额为10元的项目的10倍，因其包含的可抽取的货币单元是后者的10倍。总体而言，样本中的大额项目比小额项目多。从这点上看，PPS抽样与分层类似，都是更侧重于记录金额更大的项目。

(2)选样方法

PPS样本可以通过运用计算机软件、随机数表等随机数法或系统选样法来获取。

①随机数法。表10 - 21列示了一个应收账款总体，其中包括累计合计数，现以该表来说明如何使用计算机软件产生的随机数选取样本。

表10 - 21应收账款总体表

总体项目（实物单元）	账面金额	累计合计数	相关的货币单元
1	357	357	1～357
2	1 281	1 638	358—1 638
3	60	1 698	1 639—1 698
4	573	2 271	1 699—2 271
5	691	2 962	2 272—2 962
6	143	3 105	2 963～3 105
7	1 425	4 530	3 106～4 530
8	278	4 808	4 531 ～4 808
9	942	5 750	4 809—5 750
IO	826	6 576	5 751—6 576
11	404	6 980	6 577—6 980
12	396	7 376	6 981—7 376

假设注册会计师想要从表10 -21的总体中，选取一个含有4个账户的PPS样本。由于规定以单位金额为抽样单位，则总体容量就是7 376，因此需要计算机程序随机生成4个数字。假定计算机程序随机生成的4个数字是：6 586、1 756、850、6 499，则包含这些随机金额的总体实物单元项目需由累计合计数栏来确定。它们分别是项目Il（包含6 577—6 980元的货币金额）、项目4（1 699～2 271元）、项目2（358—1 638元）和项目10(5 751～6 576元）。注册会计师将对这些实物单元项目进行审计，并将各实物单元项目的审计结果，应用到它们各自包含的随机货币金额上。

PPS抽样允许某一实物单元在样本中出现多次。也就是说，在前例中，如果随机数是6 586、1 756、856和6 599，则样本项目就是11、4、2和11。项目11尽管只审计一次，但在统计上仍视为2个样本项目，样本中的项目总数也仍然是4个，因为样本涉及4个货币单元。

②系统选样法。系统选样首先要将总体分为若干个由同样的货币单元构成的组，并从每一组中选择一个逻辑单元（即实物单元）。每组的货币单元数量就是选样间距。

在使用系统选样方法时，注册会计师在1和选样间距（包含该选样间距）之间选择一个随机数，这个数字就是随机起点。然后注册会计师计算总体中逻辑单元的累计账面金额。选取的第一个逻辑单元就是包含与随机起点相对应的货币单元的那个项目。然后注册会计师每隔n（n代表选样间距）个货币单元依次选取所需的抽样单元（即货币单元），并选择包含这些抽样单元的所有逻辑单元（即实物单元）。例如，如果注册会计师使用的选样间距为5 000元，他在1元和5 000元之间（含5 000元）选择一个随机数作为随机起点，假设是第2 000个货币单元。然后依次是第7 000个（2 000元+5 000元）货币单元，第12 000个（7 000元+5 000元）货币单元，以及其后整个抽样总体中每间隔n个（本例中为5 000个）的货币单元被选取。注册会计师然后对包含第2 000个、第7 000个、第12 000个……货币单元的逻辑单元实施检查。

 由于每个货币单元被选取的机会相等，逻辑单元所含的货币单元越多（即账面金额越大），被选中的机会越大。相反，较小的逻辑单元被选中的机会也较小。在PPS系统选样法下，金额等于或高于选样间距的所有逻辑单元肯定会得选中。而规模只有选样间距的一半的逻辑单元被选中的概率为50%。

如果某逻辑单元的账面金额超过选样间距，它可能不止一次地被选中。如果出现这种情况，注册会计师忽略重复的选择，而且在评价样本结果时只考虑一次该逻辑单元。由于账面金额超过选样间距的逻辑单元可能被选中不止一次，实际检查的逻辑单元数量可能小于计算的样本规模。评价样本结果时对此要加以考虑，即将这些逻辑单元作为单个重大项目，其中发现的错报不需推断。

（3）可能存在的问题

PPS抽样的样本选取会出现量的问题，一个问题是：在选样时，账面余额为零的总体项目存在没有被选中的机会，尽管这些项目可能含有错报。另外，严重低估的小余额项目被选入样本的机会也很小。对此，如果注册会计师关注这些余额为零或较小的项目，那么解决这一问题的方法是对它们进行专门的审计测试。

另一个问题：PPS抽样选取的样本中无法包括负余额，如应收账款的贷方余额等。在进行选样时，可以先不考虑这些负余额，而后用其他方法去测试它们。另一种替代方法就是将它们视同为正余额，加入到所要测试的货币金额总数中，但这样做会使分析过程变得复杂化。

5．推断总体

使用PPS抽样时，注册会计师应根据样本结果推断总体错报，并计算抽样风险允许限度。如果样本中没有发现错报，推断的总体错报就是零，抽样风险允许限度小于或等于设计样本时使用的可容忍错报。在这种情况下，注册会计师通常不需进行额外的计算就可得出结论，在既定的误受风险下，总体账面金额高估不超过可容忍错报。如果样本中发现了错报，注册会计师需要计算推断的错报和抽样风险允许限度。

(1)错报比例

如果在实物单元中发现了错报，注册会计师要计算该实物单元的错报比例（用t表示），即用该实物单元中的错报金额除以该实物单元的账面金额。

t代表该实物单元包含的每一个货币单元中存在的错报金额，它也为注册会计师提供了与所抽取的货币单元中存在的错报有关的信息。例如，如果某客户账户余额的账面金额是100元，其中有50元是高估（即审定金额为50元），那么该账户余额的错报比例是：

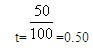
注册会计师可以说该账户余额中的每一货币单元都存在0. 50元的错报。在PPS抽样中，注册会计师在推断总体错报时需要使用样本中存在错报的货币单元的错报比例这一数据(t)。注册会计师首先将错报分为高估错报和低估错报两组，然后两组分别按降序排列错报比例。例如，如果两个高估错报的错报比例分别为0. 37和0.42，不管错报的金额如何，将0.42作为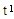，将0.37作为。

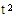(2)推断总体

完成排序后，注册会计师使用泊松分布评价特定抽样风险水平下货币单元的抽样结果。注册会计师应当计算在一定的保证水平下总体中的错报上限，并判断总体是否存在重大错报。在会计总体中，错报就是泊松分布中的事件，而内部控制系统就是泊松分布中的过程。泊松分布可以计算出，对于特定的风险水平，在组成样本的n个抽样单元中有x个发生了某事件时，总体中任一规模为n的样本发生该事件的最大频率（用MFx表示），即任意n个项目最多发生MF。次该事件。因此，泊松分布可以告诉注册会计师，在一定的风险水平下，如果样本中发现了x个错报，任一规模为n的样本中可能存在的最大错报(MF，)是多少，或者说任意n个样本项目最多发生MF。个错报。本节表10 - 19中的风险系数就是规模为n的样本在特定误受风险水平下的最大错报数量(MF。)，注册会计师用MFx除以样本规模n，得到的就是每个项目的错报最大发生率，并用其推断总体。

表10 - 22从表10 - 19中选取了几个数字，以举例说明当样本规模为50时，在不同的抽样风险水平下一定的错报数量所对应的错报最大发生率。表1O -22表示，如果在50个样本中没有发现错报，当误受风险为5%时，任意50个样本项目中存在的错报不超过3.00个（从表10 - 19中查得），每个项目发生错报的比率不超过6. 0%（即3.00÷50）；当误受风险为10%时，任意50个样本项目中存在的错报不超过2. 31个（从表10 - 19中查得），每个项目发生错报的比率不超过4. 62%（即2.31÷50）。如果在50个样本中发现了1个错报，那么当误受风险为5%时，任意50个样本项目中存在的错报不超过4.75个（从表10 - 19中查得），每个项目发生错报的比率不超过9.5%(即4.75÷50)；当误受风险为10%时，任意50个样本项目中存在的错报不超过3.89个（从表10 - 19中查得），每个项目发生错报的比率不超过7.78%(即3.89÷50)。

表10 -22 错报最大发生率表

发生错报的数量	风险水平（误受风险）	错报最大发生率（MF/50）
0	5%	6. O% ( 3. 00÷50)
O	10%	4. 62% ( 2. 31 ÷50)
l	5%	9. 5% (4. 75 ～÷50)
1	10%	7. 78% ( 3. 89 ～÷50)

错报最大发生率并不能直接提供总体中可能存在的错报金额的信息，注册会计师还需要将错报发生率转换为金额。假设某总体包含Ⅳ个抽样单元，如果在样本的n个货币单元中发现了x个错报，那么计算的既定风险水平下每个抽样单元存在错报的最大比率就是MF./n,。

注册会计师可以推断，总体中存在高估错报的抽样单元的数量不超过：

总体高估错报的最大数量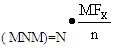

如果这些抽样单元中的错报金额最大是X，那么估计总体高估错报最大金额是：

总体高估错报的最大金额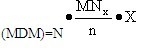

对PPS样本而言，账面金额(BV)就是总体中包含的项目（货币单元）数量，每一货币单元可能发生的最大高估错报是1元（即PPS抽样要求任一项目错报金额不能超过账面金额）。既然N=BV、X=l，则估计的总体高估错报上限是：

 总体高估错报上限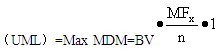

但是，这样计算出来的总体高估错报上限假设总体中每一错报的错报比例均为100%（即实际金额为0），而在许多抽样中，并非所有错报的错报比例都是100%。为了提高预计总体错报上限的准确度，注册会计师可以利用从样本中发现的其他信息和泊松分布中MF，累积增加的特点，对上述总体高估错报上限的点估计值进行修正。

首先，如果样本中没有发现错报，注册会计师估计的总体错报上限（当没有错报时称为“基本界限”）是：

“基本界限”表示，不管样本结果如何，注册会计师在给定的风险水平下估计的总体错报上限总是不会低于这个“基本界限”。在预计总体错报为0时，“基本界限”实际上等于可容忍错报。如果在样本中发现了1个错报，估计的总体错报上限就会大于这个“基本界限”。实际上，由于发现了1个错报而增加的总体错报上限点估计值是：

此时，总体错报上限的点估计值等于基本界限与样本中发现1个错报所增加的错报上限之和，即：

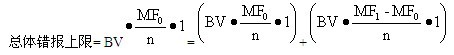
如果在样本中发现了两个错报，总体错报上限的点估计值就等于基本界限加上发现第1个错报的额外影响再加上发现第2个错报的额外影响，即：

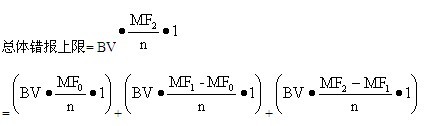
当假设每个货币单元的高估错报金额是1元时，泊松分布MF值的累积性质对在基本界限上增加的部分并不重要。但是，如果PPS样本中的额外信息（如错报比例t）也加以使用的话，这种累积性质就非常重要。注册会计师可以利用按相对大小排序的高估错报比例(t)来估计总体高估错报上限。由于高估错报不超过1元，基本界限仍然同上。但是，如果发现1个错报的错报比例是t，发现这个错报的额外影响就是：

如果发现了两个错报，它们的排序会影响其对总体错报上限点估计值的额外影响。令表示排在第一（从高到低）的错报比例，表示排在第二的错报比例，那么：

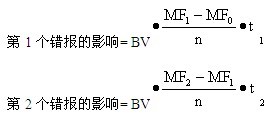
使用错报比例t计算的总体错报上限点估计值将是特定风险水平下最保守的估计值。

为了举例说明这种评价方法，假设应收账款账面金额为100 000元。如果规模为100的样本中包含2个高估错报，且f．=0.8，t：=0.5，误受风险为5%时的总体错报上限点估计值是：

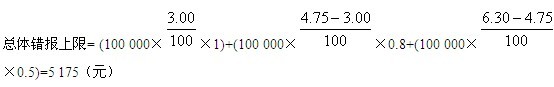
用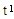，计算的第1个错报的影响是( 100 000×1.75/100×0.8)，等于1 400元；用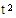计算的第2个错报的影响是( 100 000×1.55/100×0.5)，等于775元。

推断总体错报计算如表10 - 23所示。

表10 - 23 推断错报计算表

错报序号	错报比例(t)	抽样间隔	推断错报
1	0.8	1 000元	800元
2	0.5	1 000元	500元
推断错报合计			1 300元

总体错报上限点估计值中包含了这部分推断错报。

如果在样本中既发现了高估错报又发现了低估错报，注册会计师可以根据发现的低估错报调整总体错报上限点估计值。

调整的总体错报上限=总体错报上限-低估错报最佳估计值

 

但是，如果在测试高估错报时在样本中发现了大量低估错报，注册会计师应当引起注意，考虑是否使用其他抽样方法单独进行低估测试。

三、PPS抽样示例

本部分举例说明在测试高估错报时使用PPS抽样的主要步骤和方法。

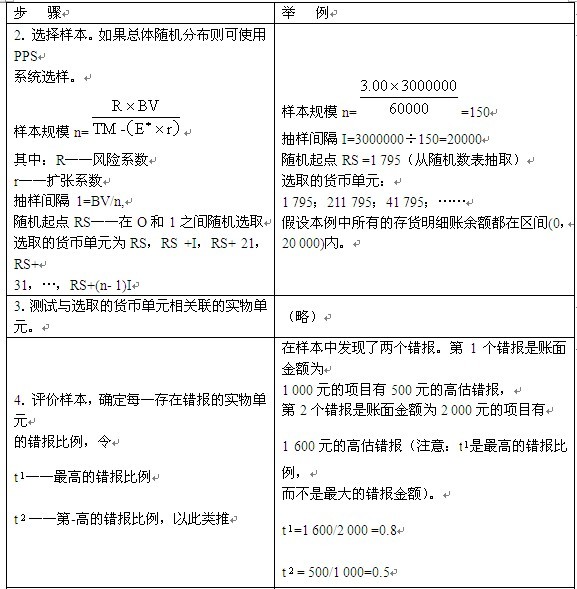
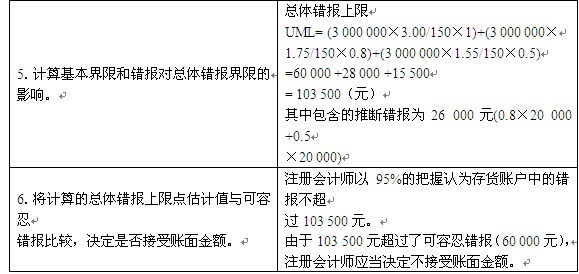
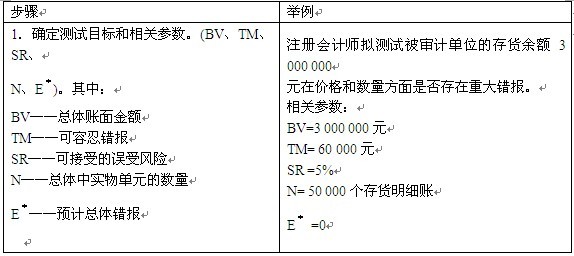
假定注册会计师在审计ABC公司时，使用PPS抽样方法测试ABC公司20 x9年12月31日的存货余额。20 x9年12月31日ABC公司的存货账户余额为3 000 000元。用BV表示总体账面金额，则有BV =3 000 000元。注册会计师确定的可接受误受风险（SR）为5%，可容忍错报（TM）为60 000元，预计总体错报(E*)为0。拟测试的存货账面金额由50 000个明细账组成，即总体中实物单元的数量Ⅳ= 50 000。

我们使用样本规模公式来确定所需的样本规模，即：

在上述公式中，总体账面价值（即账面金额BV）、可容忍错报（TM）和预计总体错报(E')已经确定。我们用R表示误受风险的风险系数（由表10 - 19查取），用r表示预计总体错报的扩张系数，则样本规模就是：

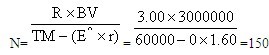
在本例中，假设所有的存货明细账余额都小于20 000元，即没有超过抽样间隔的实物单元。如果有实物单元超出抽样间隔，应当对这些实物单元进行100%的检查。

注册会计师运用系统选样法选出所需的150个样本并对与其相关的实物单元进行测试后，在样本中发现了2个错报。第一个错报是账面金额为1 000元的项目有500元的高估错报，错报比例为0.8；第二个错报是账面金额为2 000元的项目有1 600元的高估错报，错报比例为0.5。注册会计师将错报比例从

大到小排序，则有：

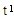=1 600/2 000=0.8

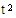= 500/1 000=0.5

注册会计师利用样本错报的相关信息计算总体错报上限的估计值，其步骤如下：

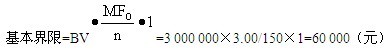
第1个错报所增加的错报上限=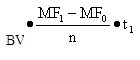=3 000 000×(4.75-3.00)/150×0.8=28 000（元）

第2个锘报所增加的错报上限=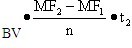 =3 000 000×(6.30-4.75)/150 x0.5 =15 500（元）

总体错报上限=基本界限+第1个错报所增加的错报上限+第2个错报所

增加的错报上限=60 000 +28 000 +15 500 =103 500（元）

由于计算的总体错报上限103 500元超过了可容忍错报（60 000元），注册会计师决定不接受账面金额，并扩大样本规模进行进一步检查。

表10 - 24  PPS抽样的应用

续表