三、最优存货量的确定
(一) 经济经货模型
经济订货模型是建立在一系列严格假设基础上的。这些假设包括：(1) 存货总需求量是已知常数；(2) 订货提前期是常数；(3) 货物是一次性入库；(4) 单位货物成本为常数，无批量折扣；(5) 库存持有成本与库存水平呈线性关系；(6) 货物是一种独立需求的物品，不受其他货物影响。
【例5-9】假设某公司每年所需的原材料为104 000件。即每周平均消耗2 000件。如果我们每次订购10 000件，则可够公司5周的原材料需要。5周后，原材料存货降至零，同时一批新的订货又将入库。这种关系可参考图5-6(a)。现设公司决定改变每次订货量为5 000件。这样，每次订货只能供公司两周半生产所需，订货的次数较前者增加了一倍，但平均库存水平元只有前者一半，可参考图5-6(b)。
本例中，存货的相关成本表现为订货成本和持有成本。订货成本与订货次数成本正比关系，而持有成本则与存货平均水平成正比关系。设公司每次订货费用为20元，存货年持有费率为每件0.8元。则与订货批量有关的存货的年总成本TIC：
TIC = 20×104000/Q+Q/2*0.8
式中：Q——每次订货批量。
我们的目的是要使公司TIC最小化。由此例，我们可抽象出经济订货模型。存货的总成本为：
TIC = K×D/Q+Q/2*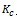
式中：TIC——与订货批量有关的每期存货的总成本；
D——每期对存货的总需求；
Q——每次订货批量；
K——每次订货费用；
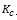——每期单位存货持有费率。
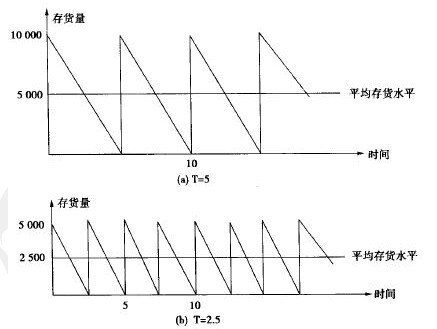
图5-6 存货水平与订货
使TIC最小的批量Q即为经济订货批量EOQ。利用数学知识，可推导出：
EOQ =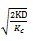 
TIC = 
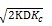
从该公式，我们可算出公司的经济订货批量和最小存货成本：
EOQ =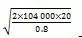 
= 2 280.35(件)
TIC =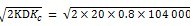 
= 1 824.28(元/件)
订货批量存货与成本、订货费用、持有成本的关系如图5-7所示。
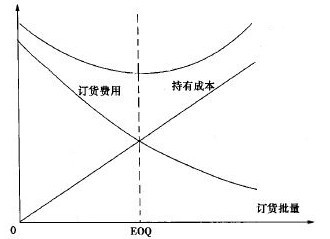
图5-7 存货总成本与订货批量的关系
有很多方法来扩展经济订货模型，以使其适用范围更广。事实上，许多存货模型研究都是立足于经济订货模型，但扩展了其假设。
(二) 保险储备
前面讨论的经济订货量是以供需稳定为前提的。但实际情况并非完全如此，企业对存货的需求量可能发生变化，交货时间也可能会延误。在交货期内，如果发生需求量增大或交货时间延误，就会发生缺货。为防止由此造成的损失，企业恶英有一定的保险储备。图5-8显示了在具有保险储备时的存货水平。图中，在再订货点，企业按EOQ订货。在交货期内，如果对存货的需求量很大，或交货时间由于某种原因被延误，企业可能发生缺货。为防止存货中断，再订货点应等于交货期内的预计需求与保险储备之和。即：
再订货点= 预计交货期内的需求＋保险储备
企业应保持多少保险储备才合适？这取决于存货中断的概率和存货中断的损失。较高的保险储备可降低缺货损失，但也增加了存货的持有成本。因此，最佳的保险储备应该是使缺货损失和保险储备的持有成本之和达到最低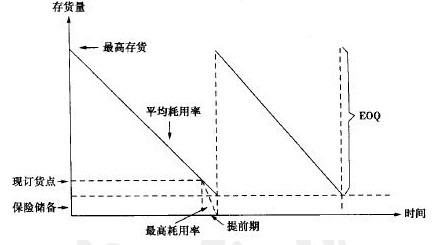
图5-8 不确定需求和保险储备下的存货水平
【例5-10】信达公司计划年度耗用某材料100 000千克，材料单价50元，经济订货量25 000千克，全年订货4次(100 000/25 000)，订货点为1 200千克。单位材料年持有成本为材料单价的25%，单位材料缺货损失24元。在交货期内，生产需要量及其概率如下：
生产需要量(千克) 概率
1 000 0.1
1 100 0.2
1 200 0.4
1 300 0.2
1 400 0.1
该公司最佳保险储备的计算如表5-7所示。
表5-7 保险储备分析 金额单位：元
|
保险储备量 |
缺货量 |
缺货概率 |
缺货损失 |
保险储备的持有成本 |
总成本 |
|
0 |
0 |
0.1 |
0 |
|
|
|
|
0 |
0.2 |
0 |
|
|
|
|
0 |
0.4 |
0 |
|
|
|
|
100 |
0.2 |
4×100×0.2×24 = 1 920 |
|
|
|
|
200 |
0.1 |
4×200×0.1×24 = 1 920 缺货损失期望值 3 840 |
0 |
3 840 |
|
100 |
0 |
0.1 |
0 |
|
|
|
|
0 |
0.2 |
0 |
|
|
续表
|
保险储备量 |
缺货量 |
缺货概率 |
缺货损失 |
保险储备的持有成本 |
总成本 |
|
|
0 |
0.4 |
0 |
|
|
|
|
0 |
0.2 |
0 |
|
|
|
|
100 |
0.1 |
4×100×0.1×24 = 960 缺货损失期望值 960 |
100×50×0.25 = 1 250 |
2 210 |
|
200 |
0 |
0.1 |
0 |
|
|
|
|
0 |
0.2 |
0 |
|
|
|
|
0 |
0.4 |
0 |
|
|
|
|
0 |
0.2 |
0 |
|
|
|
|
0
|
0.1
|
0 缺货损失期望值 0 |
200×50×0.25 = 2 500 |
2 500 |
注：缺货损失= 每年订货次数×缺货数量×缺货概率×单位缺货损失
从表5-7可以看出，当保险储备为100千克时，缺货损失与持有成本之和最低。因此，该企业保险储备量为100千克比较合适。
上例说明了考虑交货期间生产需求量时的最佳保险储备量的确定方法。至于因延误供货引起的缺货可以通过估计延误时间和平均每日耗用量来计算增加的保险储备量。
库存管理不仅需要各种模型帮助确定适当的库存水平，还需要建立相应的库存控制系统。库存控制系统可以简单，也可以很复杂。传统的库存控制系统有定量控制系统和定时控制系统两种，定量控制系统是指当存货下降到一定存货水平时即发出订货单，订货数量是固定的和事先决定的。定时控制系统是每隔一固定时期，无论现有存货水平多少，即发出订货申请，这两种系统都较简单和易于理解，但不够精确。现在许多大型公司都已采用了计算机库存控制系统。当库存数据输入计算机后，计算机即对这批货物开始跟踪。此后，每当有该货物取出时，计算机就及时作出记录并修正库存余额。当库存下降到订货点时，计算机自动发出订单，并在收到订货时记下所有的库存量。计算机系统能对大量种类的库存进行有效管理，这也是为什么大型企业愿意采用这种系统的原因之一。对于大型企业，其存货种类数以十万计，要使用人力及传统方法来对如此众多的库存进行有效管理，及时调整存货水平，避免出现缺货或浪费现象简直是不可能的，但计算机系统对此能作出迅速有效的反应。
 |
以上信息有错误 |  |
 |
